Find dropping point of an egg

Problem

You are given a 2-D grid where each cell has a value of either 1 or -1. Each cell in the box has a diagonal board that spans two corners and can redirect an egg to the right or left. A board that redirects the egg to the right spans the top-left corner to the bottom-right corner and is denoted by the number 1 in the grid. A board that redirects the egg to the left spans the top-right corner to the bottom-left corner of the grid and is represented as -1.

We place one egg at the top of each box column. Each egg has the potential to become stuck in the box or fall out of the bottom. If an egg strikes a "V" shaped pattern between two boards or if a board redirects the egg into either wall of the box, it becomes stuck. The task is to return a list of columns where ith value will denote the value of the column where the egg will drop if it starts from ith column. Below is an example of the mechanism for the matrix [1, 1, -1] [1, 1, 1]

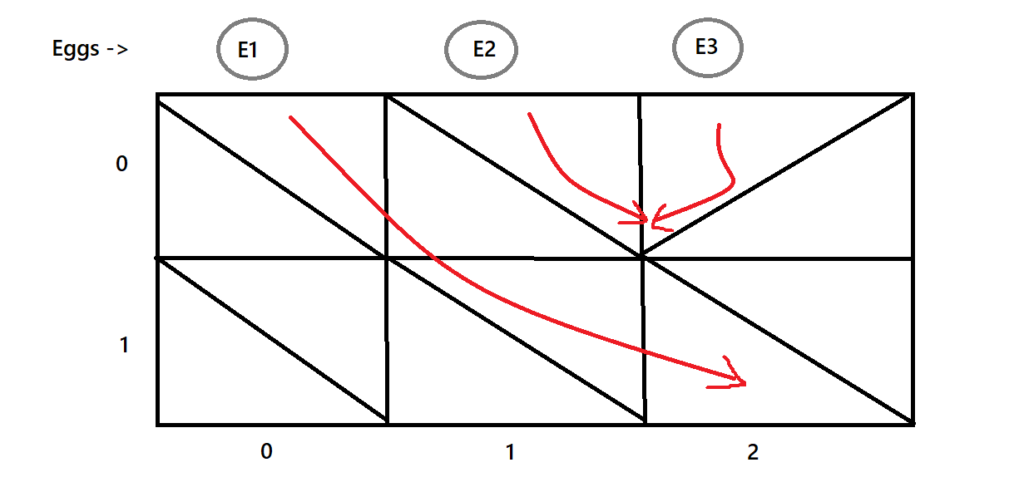
E1 will leave the grid from column 2, while E2 and E3 will both get stuck in the “V” position

Sample Input

[1, 1, -1]
[1, 1, 1]

Sample Output

[2, -1, -1]

Approach

When we are at a cell (row, col) that has the val value 1, this cell will take us to the cell (row+1, col+1), while if we are at a cell (row, col) that has the value -1, this cell will take us to the cell (row+1, col-1). We keep taking the egg down according to the above conditions. We just need to handle the cases below, as they will block the egg from going down. If we find any of the below conditions, while we are a cell, we cannot go beyond the current cell.

1. If the cell is -1 and we are at the 0th column, we cannot go beyond.
2. If the cell is 1 and we are at the last column, we cannot go beyond.
3. If we are at -1 and the left cell is 1, this is a “V” state, we cannot go beyond.
4. If we are at 1 and the right cell is -1, this is a “V” state, we cannot go beyond.

Complexity Analysis

The time complexity is O(MXN) and the space complexity is O(N).

C++ Programming

#include<bits/stdc++.h>
using namespace std;

// function to get finishing columns
vector<int> solve(vector<vector<int>>& grid) {

        int m = grid.size(), n = grid[0].size();
        vector<int> res;

        // iterate through columns
        for (int i = 0; i < n; ++i) {
            int col = i, i2;

            // iterate diagonally
            for (int j = 0; j < m; ++j) {
                i2 = col + grid[j][col];
                // check condition
                if (i2 < 0 || i2 >= n || grid[j][i2] != grid[j][col]) {
                    col = -1;
                    break;
                }
                col = i2;
            }
            res.push_back(col);
        }
        return res;
    }
    
int main()
{
    vector<vector<int>>grid {{1, 1, -1}, {1, 1, 1}};

    vector<int>ans = solve(grid);

    for(auto itr: ans) cout<<itr<<" ";
}

Output

2 -1 -1 

Java Programming

class Solution
{

// function to get finishing columns
public static int[] solve(int[][] grid) {
        int m = grid.length, n = grid[0].length, res[] = new int[n];
        
        // iterate through columns
        for (int i = 0; i < n; ++i) {
            int col = i, i2;
            
            // iterate diagonally
            for (int j = 0; j < m; ++j) {
                i2 = col + grid[j][col];
                
                // check condition
                if (i2 < 0 || i2 >= n || grid[j][i2] != grid[j][col]) {
                    col = -1;
                    break;
                }
                col = i2;
            }

            res[i] = col;
        }
        return res;
}

public static void main(String[] args)
    {
        int[][] grid = new int[2][3];
        grid[0][0] = 1;
        grid[0][1] = 1;
        grid[0][2] = -1;
        grid[1][0] = 1;
        grid[1][1] = 1;
        grid[1][2] = 1;
        int[] ans = solve(grid);
        
        for(int i=0;i<3;i++) System.out.print(ans[i]+" ");

}
}

Output

2 -1 -1 

Python Programming

# function to get finishing columns
def solve(grid):
    m, n = len(grid), len(grid[0])

    def test(i):
        # iterate diagonally
        for j in range(m):
            i2 = i + grid[j][i]

            # check condition
            if i2 < 0 or i2 >= n or grid[j][i2] != grid[j][i]:
                return -1
            i = i2
        return i

    return map(test, range(n))

grid = [[1, 1, -1], [1, 1, 1]]

for i in solve(grid):
    print(i, end=" ")

Output

2 -1 -1

People are also reading:

• Find K-th Smallest Element in BST
• Check if directed graph is connected
• Nth root of M
• Find MSB
• Longest Substring without repeating characters
• Count subarrays with given XOR
• Delete Nodes And Return Forest
• Majority Element
• Rearrange an array such that arr[i] = i
• The Stock Span Problem