In this tutorial, we will discuss matrix in Python, and we also scratch some basics of the Python NumPy module.
What is a Matrix?
In general, a matrix is a mathematical concept to represent equations in a 2-D structure, using rows and columns.
What is Python Matrix?
A Python matrix is an array of arrays. In Python, we have the list data structure as an alternative for arrays, that's why we can define a matrix as a list of lists. A Python matrix only follows a two-dimensional structure, which means it stores the data in rows and columns, and the number of columns will be the same for each row. In a matrix, the Horizontal entries are the rows and the Vertical are the columns.
Example 1
[
[1,2,3],
[4,5,6],
[7,8,9],
[10, 11, 12]
]
The above structure is a matrix, and it has 4 rows and 3 columns.
Example 2
# list approach to make a Matrix
matrix = [[1,2,3,4,5],
[6,7,8,9,10],
[11,12,13,14,15]
]
In this example, we have a matrix of 3 rows and 5 columns. We can also represent the structure of the above matrix as 3X5 (rows X columns) .
Some more examples of Python matrix:
matrix = [ [1,2,3,4],
[100,200,300,400],
[1000,2000,3000,4000]
]
print("The First Row of the matrix", matrix[0])
print("The Second Row of the matrix", matrix[1])
print("The Third Row of the matrix", matrix[2])
Output
The First Row of the matrix [1, 2, 3, 4]
The Second Row of the matrix [100, 200, 300, 400]
The Third Row of the matrix [1000, 2000, 3000, 4000]
How to create Matrix in Python?
In Python, we do not have an inbuilt matrix, but we can make it using arrays or lists. The easiest way to create a matrix is by using the nested list, but as compared to arrays of other programming languages, Python lists are very slow and inefficient when it comes to matrix computation.
Matrix is generally used for heavy mathematical computation, and if we build a matrix with a Python list it will limit the operations of the matrix and also slow down the computation process. That's why whenever it comes to the Python matrix and its mathematical operations we always consider using the numpy library.
How does the Python Matrixes Work?
The Python matrix store the data in a 2-dimensional structure, like a table without any colspan or rowspan.
Example
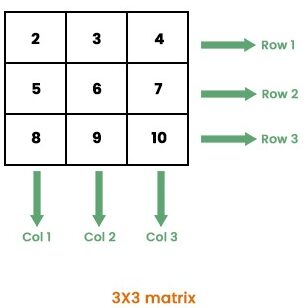
The above image is a matrix of
3X3
, which means it has 3 rows and 3 columns. We can read this metric in two ways row-wise or columns wise. If we read it row-wise we can read the complete matrix in 3 rows,
[2,3,4]
,
[5,6,7]
and
[8,9,10]
.
Similarly, we can read the complete matrix as columns-wise
[2,5,8]
,
[3, 6, 9]
and
[4, 7, 10]
. In Python, we can represent the above matrix using a list of lists or a numpy array such as.
#list matrix
matrix = [
[2,3,4],
[5,6,7],
[8,9,10]
]
1. How to create a matrix in Python using a list?
To create a matrix using a list we can use the nested list.
Example
#create a matrix using list
list_matrix = [
[12,13,14],
[15,16,17],
[18,19,20]
]
print(list_matrix)
Output
[[12, 13, 14], [15, 16, 17], [18, 19, 20]]
How to read data from the Python matrix using a list?
To access individual items or data from a matrix we can use list indexing. The indexing starts from [0][0] and goes up to [r-1][c-1], where r is the number of rows and c is the number of columns.
Example 1
Access the second row and second column value from a 3X3 list matrix in Python
#create a matrix using list
list_matrix = [
[12,13,14],
[15,16,17],
[18,19,20]
]
# second row and second column value
print("list_matrix[1][1]=",list_matrix[1][1])
Output
list_matrix[1][1]= 16
Example 2
Access all the diagonal elements from a square matrix in Python
A square matrix has two diagonals, from left to right and from right to left. In the left to the right diagonal access, the value of row and column is the same.
#create a matrix using list
list_matrix = [
[12,13,14],
[15,16,17],
[18,19,20]
]
rows = len(list_matrix)
columns = len(list_matrix[0])
# access list matrix diagonal values
print("list_matrix diagonal values")
for r in range(rows):
for c in range(columns):
#access the diagonal values
if r == c:
print(list_matrix[r][c])
Output
list_matrix diagonal values
12
16
20
In the diagonal value from right to left, the sum of both the rows and columns for these values is always equal to n-1 where n is the number of rows or columns in a square matrix.
#create a matrix using list
list_matrix = [
[12,13,14],
[15,16,17],
[18,19,20]
]
rows = len(list_matrix)
columns = len(list_matrix[0])
# access list matrix diagonal values
print("list_matrix diagonal values")
for r in range(rows):
for c in range(columns):
#access the diagonal values from right to left
if r + c==rows-1:
print(list_matrix[r][c])
Output
list_matrix diagonal values
14
16
18
Example 3
Access all the last elements from each row
To access the last element from each row we can loop over each row and access its last element.
#create a matrix using list
list_matrix = [
[12,13,14],
[15,16,17],
[18,19,20]
]
# access list matrix last element
print("list_matrix last elements")
for row in list_matrix:
#access last element of each row
print(row[-1])
Output
list_matrix last elements
14
17
20
List matrix operations
Add nested list matrix in Python
We can not perform the direct +, -, and * operation between two list matrices in Python. So to add two matrices we have to loop through individual elements and add them together.
Example
#create a matrix using list
matrix1 = [
[12,13,14],
[15,16,17],
[18,19,20]
]
matrix2 = [
[20, 21, 22],
[23,24,25],
[26,27,28]
]
#matrix that will hold the sum of matrix 1 and matrix 2
matrix3 = [
[0,0,0],
[0,0,0],
[0,0,0]
]
#the rows and columns of all the matrix must be the same
rows =3
columns = 3
#add two matices
for i in range(rows):
for j in range(columns):
matrix3[i][j] = matrix1[i][j] +matrix2[i][j]
print("The sum of matrix1 and matrix2 is:",matrix3)
Output
The sum of matrix1 and matrix2 is: [[32, 34, 36], [38, 40, 42], [44, 46, 48]]
Subtract nested list matrix in Python
Similar to the addition we can perform the subtraction between two matrices. When we subtract two matrices m1 and m2, the dimension of both the matrix must be equal.
Example
#create a matrix using list
matrix1 = [
[12,11,10],
[13,16,14],
[17,18,29]
]
matrix2 = [
[20, 21, 22],
[23,24,25],
[26,27,28]
]
#matrix that will hold the difference of matrix 1 and matrix 2
matrix3 = [
[0,0,0],
[0,0,0],
[0,0,0]
]
#the rows and columns of all the matrix must be the same
rows =3
columns = 3
#subtract two matices
for i in range(rows):
for j in range(columns):
matrix3[i][j] = matrix1[i][j] - matrix2[i][j]
print("The difference of matrix1 and matrix2 is:",matrix3)
Output
The difference of matrix1 and matrix2 is: [[-8, -10, -12], [-10, -8, -11], [-9, -9, 1]]
Multiplication of two nested list matrices in Python
The multiplication of two matrices goes with the following syntax
for i in range(len(matrix_1_rows)):
for j in range(len(matrix_2_column)):
for k in range(len(matrix_2_rows)):
result[i][j] += matrix1[i][k] * matrix2[k][j]
Example
#create a matrix using list
matrix1 = [
[12,11,10],
[13,16,14],
[17,18,29]
]
matrix2 = [
[20, 21, 22],
[23,24,25],
[26,27,28]
]
#matrix that will hold the difference of matrix 1 and matrix 2
matrix3 = [
[0,0,0],
[0,0,0],
[0,0,0]
]
#multiplication two matices
#iterate by matrix 1 rows
for i in range(len(matrix1)):
#iterate over matrix2 coloums
for j in range(len(matrix2[0])):
#iterate over matrix2 rows
for k in range(len(matrix2)):
matrix3[i][j] += matrix1[i][k] * matrix2[k][j]
print("The multiplication matrix1 and matrix2 is:",matrix3)
Output
The multiplication matrix1 and matrix2 is: [[753, 786, 819], [992, 1035, 1078], [1508, 1572, 1636]]
2. How to create a matrix using NumPy Arrays In Python
NumPy is a third-party library for Python, which is commonly used for data science . The library contains many mathematical methods and it also supports arrays. The numPy arrays are more efficient than the standard Python array module because it allows us to perform several matrix operations, such as matrix addition, matrix multiplication, and matrix subtraction.
Example
from numpy import array
arr = array([2,4,8,12,26])
print(arr)
print(type(arr)
Output:
[ 2 4 8 12 26]
<class 'numpy.ndarray'>
As standard Python does not come with the NumPy library, you have to download and install it on your system using the pip command.
Terminal command to install NumPy:
pip install numpy
How to create a matrix using a numpy array?
In NumPy , we have various methods to create arrays and matrices (array of arrays). We will discuss them one by one as follows:
- Use the simple NumPy array() method to create an array and a matrix
Example:
from numpy import array
arr = array([2,4,8,12,26])
print("The array is: \n", arr)
matrix = array([[1,2,3], [4,5,6], [7,8,9]])
print("The matrix is: \n",matrix)
Output:
The array is:
[ 2 4 8 12 26]
The matrix is:
[[1 2 3]
[4 5 6]
[7 8 9]]
- Use the NumPy zeros() method to create an array or matrix
Example:
from numpy import zeros
arr_of_zeros = zeros((1,5)) # here 1 is number of rows and 5 is number of columns
print("Array is:")
print(arr_of_zeros)
matrix_of_zeros = zeros((3,3)) # it would create a 3X3 matrix
print("Matrix is: ")
print(matrix_of_zeros)
Output:
Array is:
[[0. 0. 0. 0. 0.]]
Matrix is:
[[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]]
- Use the NumPy ones() method to create an array or matrix, where each element would be 1
Example:
from numpy import ones
arr_of_ones = ones((1,5)) # here 1 is number of rows and 5 is number of columns
print("Array is:")
print(arr_of_ones)
matrix_of_ones = ones((3,3)) # it would create a 3X3 matrix
print("Matrix is: ")
print(matrix_of_ones)
Output:
Array is:
[[1. 1. 1. 1. 1.]]
Matrix is:
[[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]]
- Use the NumPy arange () and reshape() methods to create an array and a matrix, respectively
The arange() method accepts an integer value and creates an array containing numbers from 0 to the passed integer value. The reshape() method converts the array into a matrix. It accepts two arguments representing the number of rows and columns.
Example :
from numpy import arange, reshape
arr = arange(10)
matrix = arr.reshape( (5,2))
print(arr)
print(matrix)
Output:
[0 1 2 3 4 5 6 7 8 9]
[[0 1]
[2 3]
[4 5]
[6 7]
[8 9]]
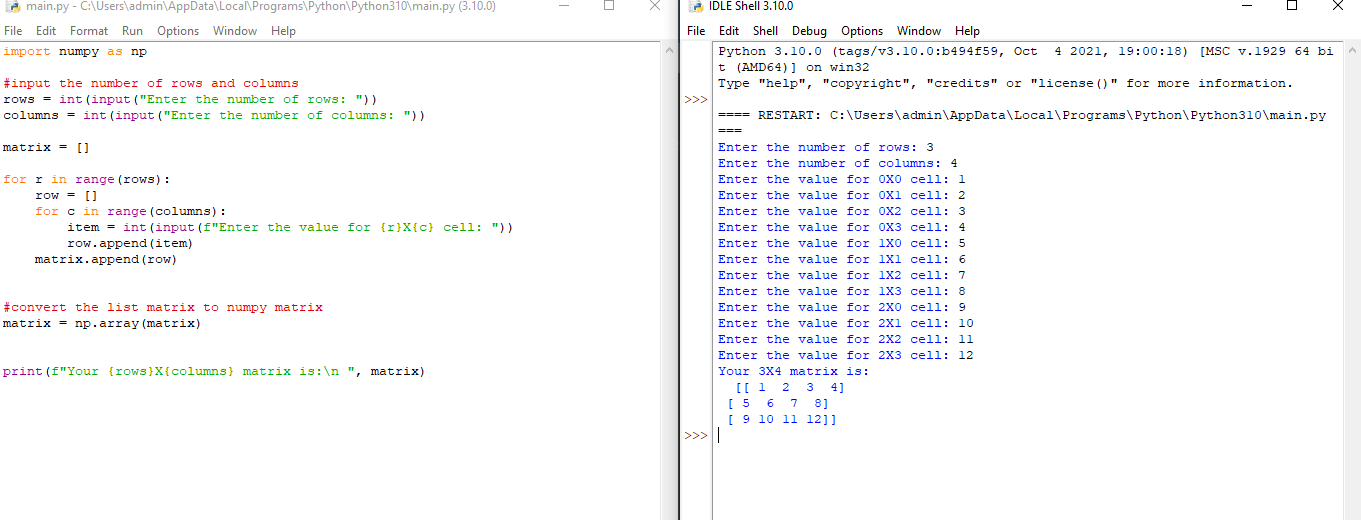
How to create a matrix in Python with user input
In the above examples, we learned how can we create a numpy matrix in Python using the array, and reshape methods. But there we statically define the items for the matrix. Now let's create a script in Python that accepts the input from the user and create the appropriate matrix.
Steps to create a matrix in Python using user input
- Import the numpy module as np
- ask the user to enter the number of rows and columns for the matrix.
- initialize an empty list matrix that we will convert to a numpy matrix later in the program.
- Create a nested loop r and c , the outer loop r will represent the rows, and the inner loop c, columns.
- Inside the outer loop initialize an empty list row that will hold the values for each row column.
- Inside the inner loop ask the user to enter the value for the matrix.
- Append the user input value to the row list.
- And outside the inner loop and inside the outer loop append the row list to the matrix.
- Outside the loop convert the Python list matrix to numpy matrix using Python numpy.array() function.
Example
import numpy as np
#input the number of rows and columns
rows = int(input("Enter the number of rows: "))
columns = int(input("Enter the number of columns: "))
#initialize an empty list
matrix = []
for r in range(rows):
row = []
for c in range(columns):
item = int(input(f"Enter the value for {r}X{c} cell: "))
row.append(item)
matrix.append(row)
#convert the list matrix to numpy matrix
matrix = np.array(matrix)
print(f"Your {rows}X{columns} matrix is:\n ", matrix)
Output
Enter the number of rows: 3
Enter the number of columns: 4
Enter the value for 0X0 cell: 1
Enter the value for 0X1 cell: 2
Enter the value for 0X2 cell: 3
Enter the value for 0X3 cell: 4
Enter the value for 1X0 cell: 5
Enter the value for 1X1 cell: 6
Enter the value for 1X2 cell: 7
Enter the value for 1X3 cell: 8
Enter the value for 2X0 cell: 9
Enter the value for 2X1 cell: 10
Enter the value for 2X2 cell: 11
Enter the value for 2X3 cell: 12
Your 3X4 matrix is:
[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
How to create a matrix in Python using numpy.matrix()
In all the above examples all the arrays and matrices we created are of
numpy.array
and
numpy.ndarray
data types. To create matrixes, numpy provides a dedicated
matrix()
method, that returns a 2D array from an array-like object.
Example 1
Create a Python matrix using numpy.matrix()
import numpy as np
matrix = np.matrix([
[1,2,3],
[4,5,6]])
print("The matrix is: ", matrix)
print("The type of the matrix is: ", type(matrix))
Output
The matrix is: [[1 2 3]
[4 5 6]]
The type of the matrix is: <class 'numpy.matrix'>
In the output, you can see that the matrix value has the data type of < class numpy.matrix> We only use the matrix() function when we want to create a 2-D array.
The difference between the matrix() and array() , the matrix() always creates a 2-D array even for the linear data, but with an array() , we can create ndarray including linear array.
Example
import numpy as np
linear_data = [1,2,3,4,5]
#create an ndarray using np.array()
array = np.array(linear_data)
#create a matrix using np.matrix using
matrix = np.matrix(linear_data)
print("array:")
print(array)
print("The type of array is",type(array))
print("The shape of array is:", array.shape)
print("\nmatrix:")
print(matrix)
print("The type of matrix is",type(matrix))
print("The shape of matrix is:", matrix.shape)
Output
array:
[1 2 3 4 5]
The type of array is <class 'numpy.ndarray'>
The shape of array is: (5,)
matrix:
[[1 2 3 4 5]]
The type of matrix is <class 'numpy.matrix'>
The shape of matrix is: (1, 5)
In the above example, we have created an array and a matrix from the same list " linear_data" . The linear_data is a list of single rows, the np.array() function converted it into a linear array of size 5, and the np.matrix() converted it into a matrix of 1 row and 5 columns.
Matrix Operations
Like the matrix in mathematics, we can apply different arithmetic operations on the matrices created with NumPy arrays. We can perform matrix operations like matrix addition, matrix transpose, matrix subtraction, and matrix multiplication.
1. Matrix Addition
We can only add two matrices if they have the same number of rows and columns. To add two matrices we can use the Arithmetic “ +” operator.
Example:
import numpy as np
A = np.array([ [1,2,3], [4,5,6], [7,8,9]])
B = np.array([[7,8,9],[4,5,6],[1,2,3]])
print("Matrix Addtion")
print(A+B)
Output:
Matrix Addtion
[[ 8 10 12]
[ 8 10 12]
[ 8 10 12]]
2. Matrix Subtraction
We can only subtract two matrices if they have the same number of rows and columns. To subtract two matrices we can use the Arithmetic “ -” operator.
Example:
import numpy as np
A = np.array([ [1,2,3], [4,5,6], [7,8,9]])
B = np.array([[7,8,9],[4,5,6],[1,2,3]])
print("Matrix Subtraction")
print(A-B)
Output:
Matrix Subtraction
[[-6 -6 -6]
[ 0 0 0]
[ 6 6 6]]
3. Matrix Multiplication
Matrix multiplication is not similar to matrix addition or subtraction. To perform the matrix multiplication using numpy, we have to use the dot() method.
Example:
import numpy as np
A = np.array([ [1,2,3], [4,5,6], [7,8,9]])
B = np.array([[7,8,9],[4,5,6],[1,2,3]])
print("Matrix Multipication")
print(A.dot(B))
Output:
Matrix Multipication
[[ 18 24 30]
[ 54 69 84]
[ 90 114 138]]
4. Transpose a Matrix
To transpose a matrix, we can use the numpy transpose method. The transpose() method will change the rows with columns.
Example:
import numpy as np
A = np.array([ [1,2,3], [4,5,6], [7,8,9]])
print("A Transpose")
print(A.transpose())
Output:
A Transpose
[[1 4 7]
[2 5 8]
[3 6 9]]
5. Accessing Elements of a Matrix
As we know a Python matrix is a list of lists, we can use the index values to access the matrix elements.
Example:
import numpy as np
A = np.array([ [1,2,3], [4,5,6], [7,8,9]])
print("The First element of the array", A[0][0])
print("The Element at first row and third column", A[0][2])
print("The last element of the array", A[-1][-1])
Output:
The First element of the array 1
The Element at first row and third column 3
The last element of the array 9
Access the Complete Row:
We use single square brackets to access a row.
Example:
import numpy as np
A = np.array([ [1,2,3], [4,5,6], [7,8,9]])
print("The First Row is:", A[0])
print("The Second row is:", A[1])
print("The Third row is:", A[2])
Output:
The First Row is: [1 2 3]
The Second row is: [4 5 6]
The Third row is: [7 8 9]
Access the Complete Column:
To access a specific column, we use a special syntax arr[ : , column_number].
Example:
import numpy as np
A = np.array([ [1,2,3], [4,5,6], [7,8,9]])
print("The First Column is:", A[:, 0])
print("The Second Column is:", A[: , 1 ])
print("The Third Column is:", A[: ,2])
Output:
The First Column is: [1 4 7]
The Second Column is: [2 5 8]
The Third Column is: [3 6 9]
6. Slicing a Numpy Array
The way we slice a Python list, we can use the same syntax in a numpy array to slice the elements. With slicing, we can access different array elements with ease.
Example:
import numpy as np
arr = np.array([1,2,3,4,5,6,7])
A = np.array([ [1,2,3], [4,5,6], [7,8,9]])
print("First 3 numbers of the array arr", arr[:3])
print("The last 3 numbers of the array arr", arr[len(arr)-3:])
Output:
First 3 numbers of the array arr [1 2 3]
The last 3 numbers of the array arr [5 6 7]
Matrix Slicing:
To slice a matrix, we use a special syntax matrix[row, columns].
Example :
import numpy as np
arr = np.array([1,2,3,4,5,6,7])
matrix = np.array([ [1,2,3], [4,5,6], [7,8,9]])
print(matrix[:2, :4]) # two rows, four columns
print("***************")
print(matrix[:1,]) # first row, all columns
print("***************")
print(matrix[:,2]) # all rows, second column
print("***************")
print(matrix[:, 2:5]) # all rows, third to fifth column
Output:
[[1 2 3]
[4 5 6]]
***************
[[1 2 3]]
***************
[3 6 9]
***************
[[3]
[6]
[9]]
7. Read the last element of each row
To only read the last element of each row, the column value would remain the same, the only thing change will be the row value.Example
import numpy as np
matrix = np.matrix(
[[1,2,3],
[4,5,6],
[7,8,9]
]
)
#last columns
total_rows = len(matrix)
print()
#read the last element from each row in Python matrix
for i in range(total_rows):
print(matrix[i, -1])
Output
3
6
9
Each element from the last row can also be seen as the last column of the matrix. We can use matrix slicing with indexing to get the last column of the matrix.
Example
import numpy as np
matrix = np.matrix(
[[1,2,3],
[4,5,6],
[7,8,9]
]
)
#last columns
total_rows = len(matrix)
#last column of the matrix
print(matrix[:, -1])
Output
matrix([[3],
[6],
[9]])
In this example the
matrix[:, -1]
will fetch the items from all the rows and -1 or last column.