Problem
Given a postfix expression, the task is to generate an expression tree from it and return the infix notation of the expression tree.
Example:
Below is the expression tree for the given expression: 2 + 3
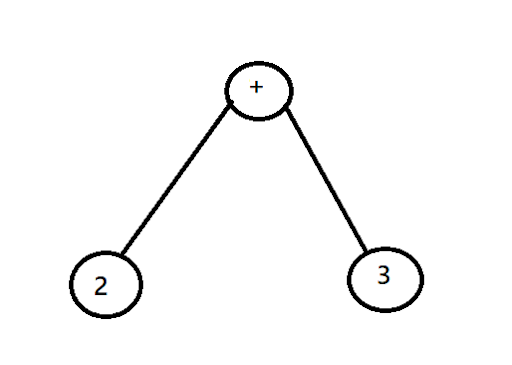
Sample Input
2 3 +
Sample Output The infix expression is
2 + 3
Explanation Below is the expression tree for the given postfix expression
+ / \ 2 3
Approach
We can traverse the given string of expressions and use a stack data structure to keep track of the previous two operands. Whenever we find an operator, just pop both of them, evaluate and push them again into the stack. The element remaining in the stack once the string finishes will be the required answer.
Complexity Analysis
The time complexity would be O(N), and the space complexity would also be O(N) due to stack.
C++ Programming
#include<bits/stdc++.h>
using namespace std;
struct TreeNode
{
char val;
TreeNode* left, *right;
};
// if character is operator
bool isOperator(char c)
{
if (c == '+' || c == '-' ||
c == '*' || c == '/' ||
c == '^')
return true;
return false;
}
// get infix expression
void inorder(TreeNode *root)
{
if(root)
{
if(isOperator(root->val)) cout<<"(";
inorder(root->left);
cout<<root->val;
inorder(root->right);
if(isOperator(root->val))
cout<<")";
}
}
// create node
TreeNode* createNode(char c)
{
TreeNode *root = new TreeNode;
root->left = root->right = NULL;
root->val = c;
return root;
};
TreeNode* getTree(char postfix[])
{
stack<TreeNode *> st;
TreeNode *root, *left, *right;
// Traverse the string
for (int i=0; i<strlen(postfix); i++)
{
// If operand
if (!isOperator(postfix[i]))
{
root = createNode(postfix[i]);
st.push(root);
}
else // if operator
{
root = createNode(postfix[i]);
// Pop two top nodes
right = st.top();
st.pop();
left = st.top();
st.pop();
// make them left and righ childs
root->right = right;
root->left = left;
// push into the stack
st.push(root);
}
}
root = st.top();
st.pop();
return root;
}
int main()
{
char postfix[] = "ab+ef*g*-";
TreeNode* r = getTree(postfix);
cout<<"The infix expression is \n";
inorder(r);
return 0;
}
Output
The infix expression is ((a + b )- ((e * f )* g ))
Java Programming
import java.util.Stack;
class Node {
char val;
Node left, right;
Node(char item) {
val = item;
left = right = null;
}
}
class Solution {
// check if character is operator
boolean isOperator(char c) {
if (c == '+' || c == '-'
|| c == '*' || c == '/'
|| c == '^') {
return true;
}
return false;
}
// do inorder traversal
void inorder(Node root) {
if (root != null) {
if(isOperator(root.val))
System.out.print("(");
inorder(root.left);
System.out.print(root.val + " ");
inorder(root.right);
if(isOperator(root.val))
System.out.print(")");
}
}
Node getTree(char postfix[]) {
Stack<Node> st = new Stack<Node>();
Node root, left, right;
// Traverse the string
for (int i = 0; i < postfix.length; i++) {
// If operand, push into stack
if (!isOperator(postfix[i]))
{
root = new Node(postfix[i]);
st.push(root);
}
else // if operator
{
root = new Node(postfix[i]);
// Pop two top nodes
right = st.pop();
left = st.pop();
// make them left and right children
root.right = right;
root.left = left;
// push the result to stack
st.push(root);
}
}
root = st.peek();
st.pop();
return root;
}
public static void main(String args[]) {
Solution TreeNode = new Solution();
String postfix = "ab+ef*g*-";
char[] charArray = postfix.toCharArray();
Node root = TreeNode.getTree(charArray);
System.out.println("The infix expression is");
TreeNode.inorder(root);
}
}
Output
The infix expression is ((a + b )- ((e * f )* g ))
Python Programming
class TreeNode:
def __init__(self , value):
self.value = value
self.left = None
self.right = None
# check if character is an operator
def isOperator(c):
if (c == '+' or c == '-' or c == '*'
or c == '/' or c == '^'):
return True
else:
return False
# do inorder traversal
def inorder(root):
if root is not None:
if(isOperator(root.value)):
print("(",end="")
inorder(root.left)
print(root.value,end=" ")
inorder(root.right)
if(isOperator(root.value)):
print(")",end="")
def getTree(postfix):
st = []
# Traverse the string
for c in postfix :
# if operand, simply push into st
if not isOperator(c):
root = TreeNode(c)
st.append(root)
# Operator
else:
# Pop two top nodes
root = TreeNode(c)
right = st.pop()
left = st.pop()
# make them children
root.right = right
root.left = left
# Add this subexpression to st
st.append(root)
# Only element will be the root of the expression tree
root = st.pop()
return root
postfix = "ab+ef*g*-"
root = getTree(postfix)
print("The infix expression is")
inorder(root)
Output
The infix expression is ((a + b )- ((e * f )* g ))
Conclusion
To convert the given postfix expression into an infix expression, we have used a stack to keep track of operands. As we have used stack, the time and space complexity would be O(N). We have implemented the given problem in three different programming languages, namely C++, Python, and Java. Moreover, we have mentioned an approach to converting a postfix expression into an infix expression.
Hopefully, this article has helped you get familiar with the code to convert a postfix expression to an infix. In case you have any queries, feel free to share them with us in the comments section below. Happy learning!
People are also reading:
- Merge Two Sorted Arrays in-place
- Subarray with Sum k
- Print all subarrays with 0 sum
- Find Maximum Subarray Sum
- Longest subarray with sum as K
- Longest? ?Bitonic? ?Subarray? ?Problem
- Rearrange an array in maximum minimum form
- The Stock Span Problem
- Find whether an array is subset of another array
- Minimum Edit Distance





Leave a Comment on this Post