Problem Statement
You are given two strings, string1 and string2, your task is to perform the operations mentioned below on string1 and determine the smallest number of edits (operations)that are required to convert ‘string1' to ‘string2'.
Operation 1: Replace
Operation 2: Remove
Operation 3: Insert
Note: All of the above operations are to be applied with equal cost only.
Example 1: Input :
String1 = ”days” String2 = “david” Output: 3
Explanation : To convert string1 to string2 we need 3 min operations, those are listed below. Operation 1: Replace the “y” with ‘V
Operation 2: Insert the “i” additionally
Operation 3: Replace the “s” with ‘d’
Example 2:
Input:
String1 = ”dell” String2 = “doll” Output: 1
Explanation: To convert the string1 to string2 we need 1 min operation, which is listed below Operation 1: Replace the “e” with ‘o’
Approach:
In the problem statement above, we are asked to calculate the Minimum Edit Distance using the given strings. So, if we pay close attention to the problem statement, we'll note that it has an ideal substructure and overlapping subproblem properties. Now, we need to discuss the unique properties i.e.
- Optimal Substructure property
- Overlapping subproblem property
Optimal Substructure property :
The Optimal Substructure Property has a given problem when the optimum solution of the problem is achieved by optimizing its sub-problems.
Overlapping Subproblem property :
Like Divide and Conquer, Dynamic Programming blends solutions to sub-problems. Only when solutions to the same subproblems are needed repeatedly, Dynamic Programming is used. In dynamic programming, computed solutions to subproblems are placed in a table so that they do not have to be recomputed again. Dynamic Programming cannot be used if there are no common (overlapping) subproblems since storing the solutions is useless if they are never used again. Time Complexity: The above solution has an exponential time complexity in the worst case
- In the worst-case scenario, we could end up performing O(3m) operations, where m is the length of string1.
- If none of the characters in two strings fit, the worst-case scenario occurs.
Note : It's important to remember to properly identify the base case; otherwise, a Recursion Depth Exceeded exception can occur.
Space Complexity:
The space complexity is O(n*d), where,
n : Is the length of the string1
d : Is the minimum number of operations required
Approach 1 (Recursion):
These types of problems can be solved with the traversal technique with recursion that is discussed below. We have two types of traversal i.,e.
- We can traverse from left to right
- We can traverse from right to left
So, on traversing, we have to concentrate on character processing. The idea behind the idea is to process each character one at a time, starting from the left or right side of both strings. If we consider the traversing from the right corner, then, for each pair of characters traversed, we will have two options.
- m: String1 length
- n: String 2 length
- If the last characters of the two strings are the same then we will ignore and move forward... As a result, we will decrement the two strings lengths m-1 and n-1 and we will apply our computation on n-1 and m-1 string lengths respectively
- Otherwise (If the last characters are not the same), then, we shall consider all the possible operations on ‘string1', and compute the minimum cost for all three operations, and take the lowest of three values. The operations are computed recursively.
Algorithm:
We will consider two-pointers, and based on the operation needed we shall apply the techniques, these are discussed below:
- Insert : Computation is applied on recursion(m, n-1)
- Remove: Computation is applied on recursion(m-1, n)
- Replace: Computation is applied on recursion(m-1, n-1)
where n are lengths of string1 and string2 Time Complexity: O(n^m) Space Complexity: O(n*m) Where n and m are respective lengths of two strings
Below is the Python Version (Recursion) :
"""A rudimentary recursive Python program to
find the smallest number of edits
required to convert the string1 to string2"""
def editminDistance(string1, string2, m, n):
# The only choice if the first string is empty is to.
# in the first string, insert all characters from the second string
if m == 0:
return n
#If the second string is empty, the only option is to remove all of the first string's characters.
if n == 0:
return m
#If the last characters of two strings are identical, there isn't anything to do. Ignore the last few characters and count the number of strings left.
if string1[m-1] == string2[n-1]:
return editminDistance(string1, string2, m-1, n-1)
#If the last characters of the first string are not the same, consider all three
# operations on the last character of the first string, recursively # compute the minimum cost for all three operations and take the lowest of the three values.
return 1 + min(editminDistance(string1, string2, m, n-1), # Insert
editminDistance(string1, string2, m-1, n), # Remove
editminDistance(string1, string2, m-1, n-1) # Replace
)
# Driver program
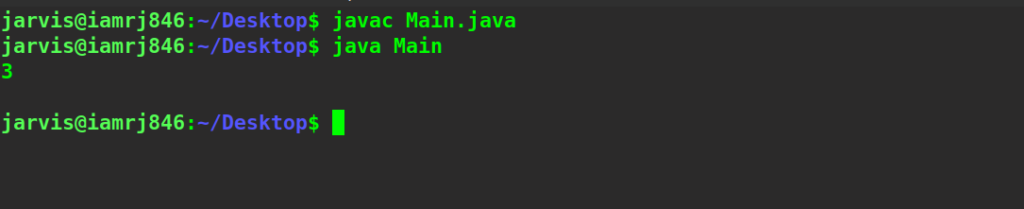
string1 = "sunday"
string2 = "saturday"
print(editminDistance(string1, string2, len(string1), len(string2)))
print()

C++ Approach (Recursion) :
// A Naive recursive C++ program to find minimum number
// edits required to convert string1 to string2
#include <bits/stdc++.h>
using namespace std;
//A utility function for determining the smallest of three numbers.
int min(int x, int y, int z) { return min(min(x, y), z); }
int editminDist(string string1, string string2, int m, int n)
{
//If the first string is empty, the only choice is to insert all of the characters from the second string.
if (m == 0)
return n;
//If the second string is of zero length, the only alternative is to delete all of the first string's characters.
if (n == 0)
return m;
// Nothing to do if the last characters of two strings are the same.
//Ignore the last few characters and count the remaining strings.
if (string1[m - 1] == string2[n - 1])
return editminDist(string1, string2, m - 1, n - 1);
//If the last characters of the first string are not the same, consider all three
// operations on the last character of the first string,
// recursively compute the minimum cost for all three
// operations, and take the lowest of the three values.
return 1+ min(editminDist(string1, string2, m, n - 1), // Insert
editminDist(string1, string2, m - 1, n), // Remove
editminDist(string1, string2, m - 1,
n - 1) // Replace
);
}
// Driver program
int main()
{
string string1 = "dell";
string string2 = "doll";
cout << editminDist(string1, string2, string1.length(),
string2.length());
return 0;
}
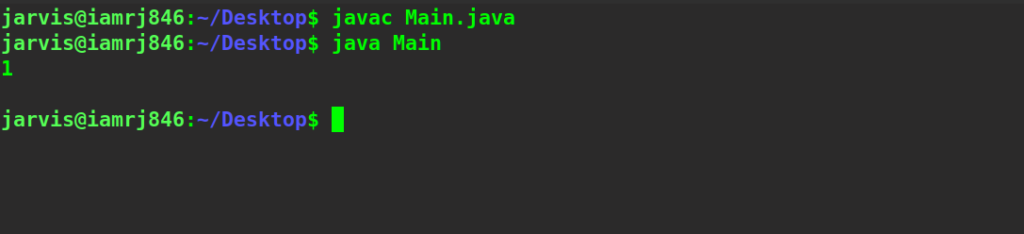
Java Version (Recursion):
// A rudimentary recursive Java code to find the number of operations required to convert string1 to string2 operations
public class main {
static int min(int x, int y, int z)
{
if (x <= y && x <= z)
return x;
if (y <= x && y <= z)
return y;
else
return z;
}
static int editminDist(String string1, String string2, int m,
int n)
{
// If the first string is empty, the only choice is to insert all of the characters from the second string.
if (m == 0)
return n;
// If the second string is zero, the only alternative is to delete all of the first string's characters.
if (n == 0)
return m;
// Nothing to do if the last characters of two strings are the same.
//Ignore the last few characters and count the remaining strings.
if (string1.charAt(m - 1) == string2.charAt(n - 1))
return editminDist(string1, string2, m - 1, n - 1);
// If the last characters of the first string are not the same, consider all
// three operations on the last character of the first
// string, recursively compute the minimum cost for all
// three operations, and take the lowest of three // values.
return 1
+ min(editminDist(string1, string2, m, n - 1), // Insert
editminDist(string1, string2, m - 1, n), // Remove
editminDist(string1, string2, m - 1,
n - 1) // Replace
);
}
// Driver program
public static void main(String args[])
{
String string1 = "sunday";
String string2 = "saturday";
System.out.println(editminDist(
string1, string2, string1.length(), string2.length()));
System.out.println();
}
}
Approach 2 (Dynamic Programming Bottom-Up)
Efficient Approach (DP)
This method is efficient. We can use the Dynamic Programming Approach with ease since the optimal overlapping property exists. The following is the main distinction between the recursive and dynamic programming approaches: We will not reuse the computed subroutine in the dynamic programming approach; instead, we will save all computed values in an array, and if we encounter the same recursive call to be computed repeatedly, we will simply use the functional value from the table. Memoization is the term for this process. To know the Efficient Approach we should first need to know why we are using this approach, this can be figured out by looking at the recursion calls picture.
Explanation of memoization from recursion call picture
Many subproblems are solved repeatedly, as shown by the fact that eD(2, 2) is named three times. This problem has the Overlapping Subproblem property since the same problems are named twice. As a result, the Edit Distance problem has both properties of a complex programming problem (Optimal substructure and overlapping subproblem). Recomputations of the same subproblems can be avoided, just by using dynamic programming. Finally, to reduce the time and space complexity we switch to efficient approaches. Algorithm for Dynamic Programming: The Complete Algorithm is identical to the recursive one, with the exception that we will declare an extra key functionality to store pre-computed values. Time Complexity : O(N*M) Space Complexity: O(N*M) Where N and M are the lengths of the Input string1 and string2.
Python Version (Dynamic Programming Bottom-Up)
# A Python program focused on Dynamic Programming to solve the edit distance problem
def editminDistDP(string1, string2, m, n):
# Make a table to keep track of subproblem outcomes.
table = [[0 for x in range(n + 1)] for x in range(m + 1)]
# Fill in d[][] from the bottom up.
for i in range(m + 1):
for j in range(n + 1):
# If the first string is void, the only choice is to # insert the entire second string.
if i == 0:
table[i][j] = j # Minimum number of operations = j
# If the second string is zero, the only choice is to delete all of the characters from it.
elif j == 0:
table[i][j] = i # Minimum number of operations = i
# If the last characters are the same, ignore the last char # and continue with the rest of the string.
elif string1[i-1] == string2[j-1]:
table[i][j] = table[i-1][j-1]
# If the last character differs, consider all
# possibilities and find the smallest number. If the last character differs, consider all
# possibilities and find the smallest number.
else:
table[i][j] = 1 + min(table[i][j-1],# Insert
table[i-1][j], # Remove
table[i-1][j-1]) # Replace
return table[m][n]
# Driver program
string1 = "doll"
string2 = "dell"
print(editminDistDP(string1, string2, len(string1), len(string2)))
print()

C++ Version (Dynamic Programming Bottom-Up) >
// A C++ programme that uses Dynamic Programming to find the smallest number of operations to convert string1 to string2.
#include <bits/stdc++.h>
using namespace std;
//A utility function for determining the smallest of three numbers.
int min(int x, int y, int z) { return min(min(x, y), z); }
int editDistDP(string string1, string string2, int m, int n)
{
// Make a table to keep track of subproblem outcomes.
int table[m + 1][n + 1];
// Fill d[][] in bottom up trend
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
// If the first string is empty, the only alternative is to insert the entire second string.
if (i == 0)
table[i][j] = j; // Min number of operations = j
// If the second string is zero, the only choice is to delete all of the characters from it.
else if (j == 0)
table[i][j] = i; // Min number of operations = i
//If the last characters are the same, forget the last char
// and continue with the rest of the string.
else if (string1[i - 1] == string2[j - 1])
table[i][j] = table[i - 1][j - 1];
//If the last character is different, consider all choices and find the minimum.
else
table[i][j]
= 1
+ min(table[i][j - 1], // Insert
table[i - 1][j], // Remove
table[i - 1][j - 1]); // Replace
}
}
return table[m][n];
}
// Driver program
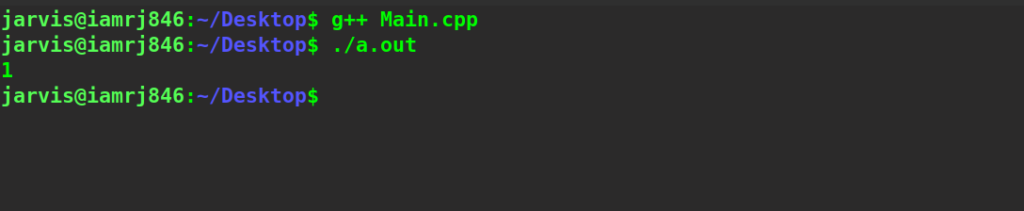
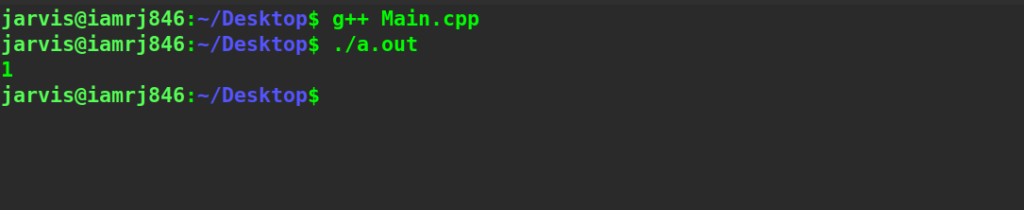
int main()
{
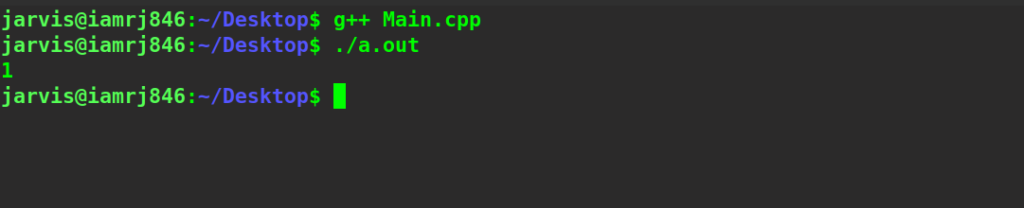
string string1 = "dell";
string string2 = "doll";
cout << editDistDP(string1, string2, string1.length(),
string2.length());
cout<<endl;
return 0;
}
Java Version (Dynamic Programming)
// A Java program that uses Dynamic Programming to find the smallest number of operations to convert string1 to string2.
public class main {
static int min(int x, int y, int z)
{
if (x <= y && x <= z)
return x;
if (y <= x && y <= z)
return y;
else
return z;
}
static int editminDistDP(String string1, String string2, int m,
int n)
{
// Make a table to keep track of subproblem outcomes.
int table[][] = new int[m + 1][n + 1];
// Fill in d[][] from the bottom up.
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
//If the first string is empty, the only alternative is to insert the entire second string.
if (i == 0)
table[i][j] = j; // Min number of operations = j
//If the second string is zero, the only choice is to delete all characters from it.
else if (j == 0)
table[i][j] = i; // Min. operations = i
//If the last characters are the same, ignore the last / char and continue with the rest of the string.
else if (string1.charAt(i - 1)
== string2.charAt(j - 1))
table[i][j] = table[i - 1][j - 1];
//If the last character is different, consider all possibilities and choose the / smallest one.
else
table[i][j] = 1
+ min(table[i][j - 1], // Insert
table[i - 1][j], // Remove
table[i - 1][j - 1]); // Replace
}
}
return table[m][n];
}
// Driver program
public static void main(String args[])
{
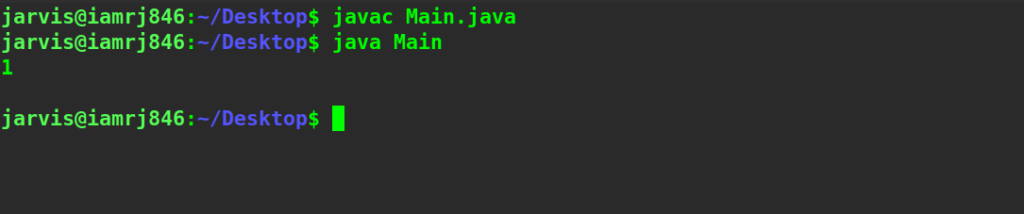
String string1 = "doll";
String string2 = "dell";
System.out.println(editminDistDP(
string1, string2, string1.length(), string2.length()));
System.out.println();
}
}
Approach 3 (Dp Top Down)
This version is completely based on the Recursion + Table approach, the implementation of this approach is discussed below.
Python Version (Top Down)
def mineditDis(s11, s22, n, m, table) :
#If one of the strings is zero, return the characters from the other string.
if(n == 0) :
return m
if(m == 0) :
return n
## To see if the recursive tree for n and m has already been run.
if(table[n][m] != -1) :
return table[n][m];
# Perform the recursive function for n-1, m-1 if the characters are equal.
if(s11[n - 1] == s22[m - 1]) :
if(table[n - 1][m - 1] == -1) :
table[n][m] = mineditDis(s11, s22, n - 1, m - 1, table)
return table[n][m]
else :
table[n][m] = table[n - 1][m - 1]
return table[n][m]
#If the characters are not equal, we must find the lowest cost of all three operations.
else :
if(table[n - 1][m] != -1) :
m1 = table[n - 1][m]
else :
m1 = mineditDis(s11, s22, n - 1, m, table)
if(table[n][m - 1] != -1) :
m2 = table[n][m - 1]
else :
m2 = mineditDis(s11, s22, n, m - 1, table)
if(table[n - 1][m - 1] != -1) :
m3 = table[n - 1][m - 1]
else :
m3 = mineditDis(s11, s22, n - 1, m - 1, table)
table[n][m] = 1 + min(m1, min(m2, m3))
return table[n][m]
# Driver code
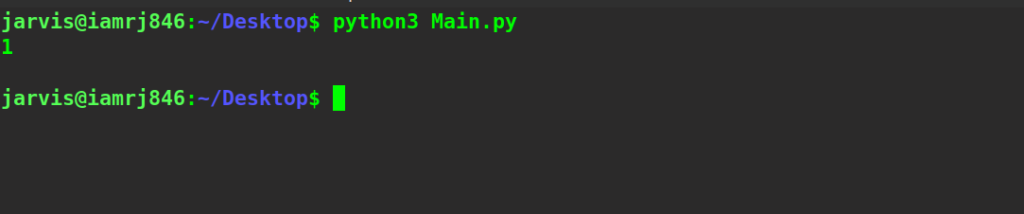
string1 = "doll"
string2 = "dell"
n = len(string1)
m = len(string2)
table = [[-1 for i in range(m + 1)] for j in range(n + 1)]
print(mineditDis(string1, string2, n, m, table))
print()
C++ Version(Top Down)
#include <bits/stdc++.h>
using namespace std;
int minDis(string string1, string string2, int n, int m, vector<vector> &dp){
//If any string is zero, return the characters from the other string.
if(n==0) return m;
if(m==0) return n;
// To see if the recursive tree for the given n and m has already been run.
if(dp[n][m]!=-1) return dp[n][m];
//If the characters are the same, run the recursive function for n-1 and m-1.
if(string1[n-1]==string2[m-1]){
if(dp[n-1][m-1]==-1){
return dp[n][m] = minDis(string1, string2, n-1, m-1, dp);
}
else
return dp[n][m] = dp[n-1][m-1];
}
//If the characters are not equal, we must compare them.
// Determine the lowest cost of all three activities.
else{
int m1, m2, m3; // temporary variables declarations
if(dp[n-1][m]!=-1){
m1 = dp[n-1][m];
}
else{
m1 = minDis(string1, string2, n-1, m, dp);
}
if(dp[n][m-1]!=-1){
m2 = dp[n][m-1];
}
else{
m2 = minDis(string1, string2, n, m-1, dp);
}
if(dp[n-1][m-1]!=-1){
m3 = dp[n-1][m-1];
}
else{
m3 = minDis(string1, string2, n-1, m-1, dp);
}
return dp[n][m] = 1+min(m1, min(m2, m3));
}
}
// Driver program
int main() {
string string1 = "dell";
string string2 = "doll";
int n= string1.length(), m = string2.length();
vector<vector> dp(n+1, vector(m+1, -1));
cout<<minDis(string1, string2, n, m, dp);
cout<<endl;
return 0;
}

Java Version (Dp Top Down)
import java.util.*;
public class main
{
static int mineditDis(String s11, String s22,
int n, int m, int[][]table)
{
//If any String is zero, return the characters from the other String.
if(n == 0)
return m;
if(m == 0)
return n;
//To see if the recursive tree exists.
//has already been executed for provided n & m
if(table[n][m] != -1)
return table[n][m];
//If the characters are the same, run the recursive function for n-1 and m-1.
if(s11.charAt(n - 1) == s22.charAt(m - 1))
{
if(table[n - 1][m - 1] == -1)
{
return table[n][m] = mineditDis(s11, s22, n - 1, m - 1, table);
}
else
return table[n][m] = table[n - 1][m - 1];
}
//If the characters are not identical, we must compare them.
// Assess the lowest cost of all three activities.
else
{
int m1, m2, m3; // temp variables
if(table[n-1][m] != -1)
{
m1 = table[n - 1][m];
}
else
{
m1 = mineditDis(s11, s22, n - 1, m, table);
}
if(table[n][m - 1] != -1)
{
m2 = table[n][m - 1];
}
else
{
m2 = mineditDis(s11, s22, n, m - 1, table);
}
if(table[n - 1][m - 1] != -1)
{
m3 = table[n - 1][m - 1];
}
else
{
m3 = mineditDis(s11, s22, n - 1, m - 1, table);
}
return table[n][m] = 1 + Math.min(m1, Math.min(m2, m3));
}
}
// Driver code
public static void main(String[] args)
{
String string1 = "dell";
String string2 = "doll";
int n= string1.length(), m = string2.length();
int[][] table = new int[n + 1][m + 1];
for(int i = 0; i < n + 1; i++)
Arrays.fill(table[i], -1);
System.out.print(mineditDis(string1, string2, n, m, table));
System.out.println();
}
}
Approach 4 ( Dp Space Optimised Solution):
In this approach, we will construct a decent space-optimized approach for this problem statement. This can be explained through the below discussion The method described above requires O(m x n) space. So by convection, If the length of the strings is greater than 2000, this will not work because it can only generate a 2D array of 2000 x 2000. Only one row, the upper row, is required to fill a row in a DP array. We only need values from the 9th row to fill the I = 10 rows in the DP array. As a result, we simply make a DP array of 2 x str1 length. This method conserves space. Below is the implementation of this approach.
Python version (Space optimized)
# a space optimised Dp solution in python version
def EditminDistDP(str11, str22):
len1 = len(str11)
len2 = len(str22)
# Make a DP array to keep track of the results of previous computations.
table = [[0 for i in range(len1 + 1)]
for j in range(2)];
#When the second String
#is zero, we delete all characters as a base condition.
for i in range(0, len1 + 1):
table[0][i] = i
# Begin to fill the DP. This loop is repeated for each character in the second String.
for i in range(1, len2 + 1):
# This loop compares the characters in the second String to the characters in the first String.
for j in range(0, len1 + 1):
#If the first String is empty, we must perform an add character operation to obtain the second String.
if (j == 0):
table[i % 2][j] = i
#If both Strings have the same character, no operation is performed. The bound # is the row number, and i% 2 is for it.
elif(str11[j - 1] == str22[i-1]):
table[i % 2][j] = table[(i - 1) % 2][j - 1]
#If a character in both Strings is not the same, we take the lowest of the three specified operations
else:
table[i % 2][j] = (1 + min(table[(i - 1) % 2][j],
min(table[i % 2][j - 1],
table[(i - 1) % 2][j - 1])))
# After filling the DP array, if len2 is even, we'll end up in the 0th row; otherwise, we'll end up in the 1st row, so we'll take len2 percent 2 # to get a row.
print(table[len2 % 2][len1], "")
print()
# Driver program
if __name__ == '__main__':
string1 = "dell"
string2 = "doll"
EditminDistDP(string1, string2)

C++ Version (Dp Space Optimized)
// A Dynamic Programming Method that Saves Space by reducing the space by the number of operations required to convert string 1 to string 2
#include <bits/stdc++.h>
using namespace std;
void EditDistDP(string str11, string str22)
{
int len1 = str11.length();
int len2 = str22.length();
// Make a DP array to keep track of the results of previous calculations.
int table[2][len1 + 1];
//To fill the DP array with zeros, use the following code.
memset(table, 0, sizeof table);
//When the second string is empty, we remove all characters as a base condition.
for (int i = 0; i <= len1; i++)
table[0][i] = i;
// Begin to fill the DP // This loop is repeated for each character in the second string.
for (int i = 1; i <= len2; i++) {
// This loop compares the characters in the second string to the characters in the first string.
for (int j = 0; j <= len1; j++) {
// If the first string is empty, we must perform an add character operation to obtain the second string.
if (j == 0)
table[i % 2][j] = i;
// If a character in both strings is the same, we don't perform any
// operations. In this case, i % 2 stands for bound
// row number.
else if (str11[j - 1] == str22[i - 1]) {
table[i % 2][j] = table[(i - 1) % 2][j - 1];
}
// If a character in both strings is not the same, we take the minimum of the three operations specified.
else {
table[i % 2][j] = 1 + min(table[(i - 1) % 2][j],
min(table[i % 2][j - 1],
table[(i - 1) % 2][j - 1]));
}
}
}
// after filling the DP array / if len2 is even, we'll end up in the 0th row; otherwise, we'll end up in the 1st row, so we'll take len2 % 2 / to get row
cout << table[len2 % 2][len1] << endl;
cout<<endl;
}
// Driver code
int main()
{
string string1 = "doll";
string string2 = "dell";
EditDistDP(string1, string2);
return 0;
}
Java version (Dp Space Optimized)
// A Java program using Space Efficient Dynamic Programming to find the smallest number of operations to convert string1 to string2.
import java.util.*;
public class Main
{
static void EditminDistDP(String str11, String str22)
{
int len1 = str11.length();
int len2 = str22.length();
int [][]table = new int[2][len1 + 1];
//When the second String is zero, we delete all characters as a base condition.
for (int i = 0; i <= len1; i++)
table[0][i] = i;
// Begin to fill the DP / This loop is repeated for each character in the second String.
for (int i = 1; i <= len2; i++)
{
// This loop contrasts the characters in the second string with the characters in the first String.
for (int j = 0; j <= len1; j++)
{
//If the first String is zero, we must perform an add character operation to obtain the second String.
if (j == 0)
table[i % 2][j] = i;
//If a character in both strings is the same, we don't perform any / operations. In this case, i 2 stands for bound / row number.
else if (str11.charAt(j - 1) == str22.charAt(i - 1)) {
table[i % 2][j] = table[(i - 1) % 2][j - 1];
}
//If a character in both Strings is not the same, we take the minimum of the three operations defined.
else {
table[i % 2][j] = 1 + Math.min(table[(i - 1) % 2][j],
Math.min(table[i % 2][j - 1],
table[(i - 1) % 2][j - 1]));
}
}
}
//after filling the DP array / if len2 is even, we'll end up in the 0th row; otherwise, we'll end up in the 1st row, so we'll take len2 % 2 / to get row
System.out.print(table[len2 % 2][len1] +"\n");
System.out.println();
}
// Driver code
public static void main(String[] args)
{
String string1 = "doll";
String string2 = "dell";
EditminDistDP(string1, string2);
}
}
Conclusion
We learned the following fundamentals in the preceding article:
- What is the optimal substructure?
- What is the property of overlapping subproblems?
We also learned the step-by-step procedure for solving the Minimum Edit Distance. Approaches we learnt In this article, we have learned the step-by-step implementation of the above problem statement in many approaches. These approaches are listed below.
- Naive Approach using Recursion.
- Dynamic Programming Approach using Top-Down trend.
- Dynamic Programming Approach using Bottom-up fashion.
- Dynamic Programming Top-Down Approach using a space-optimized solution.
We hope that you will be able to solve this problem and its variants without difficulty now.
Happy Coding!
People are also reading:
- Construct a tree from Inorder and Level order traversals
- Write a C++ Program to print a Man using Graphics
- Program to Find LCM and HCF of two numbers
- Move all zeros present in an array to the end
- Find whether an array is subset of another array
- How to find and remove loops in a Linked List?
- Find minimum jumps required to reach the destination
- Difference Between Repeater, DataList and GridView
- Bellman-Ford Algorithm
- DSA Binary Search Tree





Leave a Comment on this Post