Problem
Given an m-ary tree that can have a count of children greater than 2. Convert it into its mirror tree .
Sample Input
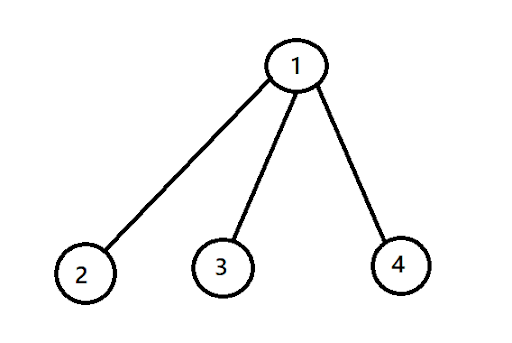
Sample Output
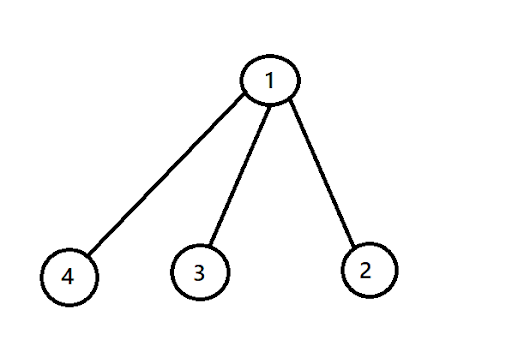
Approach
We can use “Depth First Search” to solve this problem. We can first store all the children of each node in a list. We traverse the given tree in any order and for each node reverse its children list. The reversal can be done when we backtrack.
Complexity Analysis
The time complexity would be O(N) and the space complexity would also be O(N) due to the call stack.
C++ Programming
#include<bits/stdc++.h>
using namespace std;
struct TreeNode
{
int val;
vector<TreeNode*> children;
TreeNode(int val) {
this->val = val;
}
};
// print the tree
void preOrder(TreeNode* root)
{
// base case
if (root == nullptr) {
return;
}
cout << root->val << ' ';
for (TreeNode* children: root->children) {
preOrder(children);
}
}
void solve(TreeNode* root)
{
// base case
if (!root) {
return;
}
// DFS on each child
for (TreeNode* children: root->children) {
solve(children);
}
// Reverse the order of the elements in the children
reverse(root->children.begin(), root->children.end());
}
int main()
{
TreeNode* root = new TreeNode(1);
(root->children).push_back(new TreeNode(2));
(root->children).push_back(new TreeNode(3));
(root->children).push_back(new TreeNode(4));
solve(root);
preOrder(root);
return 0;
}
Output
1 4 3 2
Java Programming
import java.util.ArrayList;
import java.util.List;
class TreeNode
{
int val;
List<TreeNode> children;
TreeNode(int val)
{
this.val = val;
children = new ArrayList<>();
}
}
class Main
{
public static void inOrder(TreeNode root)
{
// base case
if (root == null) {
return;
}
// print the current node
System.out.print(root.val + " ");
for (TreeNode children: root.children) {
inOrder(children);
}
}
public static void solve(TreeNode root)
{
// base case
if (root == null) {
return;
}
// DFS on all children
for (TreeNode children: root.children) {
solve(children);
}
// Reverse the order of the elements in the children
int n = root.children.size();
for (int i = 0, j = n - 1; i < j; i++, j--)
{
TreeNode temp = root.children.get(i);
root.children.set(i, root.children.get(j));
root.children.set(j, temp);
}
}
public static void main(String[] args)
{
// construct an m–ary tree
TreeNode root = new TreeNode(1);
(root.children).add(new TreeNode(2));
(root.children).add(new TreeNode(3));
(root.children).add(new TreeNode(4));
solve(root);
inOrder(root);
}
}
Output
1 4 3 2
Python Programming
class TreeNode: def __init__(self, val): self.val = val self.children = list() def preOrder(root): # base case if root is None: return # print the current node print(root.val, end=' ') # recur for all children nodes from left to right for c in root.children: preOrder(c) # Recursive function to convert an m–ary tree into its mirror image def swap(children, i, j): x = children[i] children[i] = children[j] children[j] = x def solve(root): # base case if root is None: return # DFS for each children for c in root.children: solve(c) # Reverse the order of the elements in the children n = len(root.children) for i in range(n//2): swap(root.children, i, n - i - 1) root = TreeNode(1) (root.children).append(TreeNode(2)) (root.children).append(TreeNode(3)) (root.children).append(TreeNode(4)) solve(root) preOrder(root)
Output
1 4 3 2
People are also reading:





Leave a Comment on this Post