Longest Palindromic Subsequence using Dynamic Programming

Problem Statement

You are given a String ‘ S’ of a certain length, your task is to find the maximum possible palindromic subsequence that can be obtained from the given string.

Subsequence

A subsequence of a given string is generated by deleting some characters of that string without changing its order.

Example 1:

Input: S = "ABBDCACB"
Output: 5

Explanation: From the above string, the Longest possible palindromic subsequence is 5, and the subsequence of the string is “BCACB”.

Example 2:

Input: S = "ANMAQRSLAGHYAGHLAM"
Output: 9

Explanation: From the above string, the longest possible palindromic subsequence is 9, and the subsequence of the string is "MALAYALAM."

Approach

In the above problem statement, we are asked to find out the maximum palindromic subsequence that can be obtained from the given string. So, if we could observe the problem statement very keenly, we can encounter that the problem has optimal substructure and overlapping subproblem properties.

Optimal Substructure

A given problem has Optimal Substructure Property if an optimal solution of the given problem can be obtained by using optimal solutions of its subproblems.

Overlapping Subproblems

Dynamic Programming, like Divide and Conquer, combines solutions to sub-problems. Dynamic Programming is primarily used when solutions to the same subproblems are required repeatedly. Computed solutions to subproblems are stored in a table in dynamic programming so that they do not have to be recomputed. So, if there are no common (overlapping) subproblems, Dynamic Programming cannot be used because storing the solutions is pointless if they are never needed again.

Approach 1: (Recursion)

This approach is called the naive approach, the idea is to implement the Recursion. For implementing the recursion, we will have two cases:

1. If the first and last characters of the strings are the same, then we increment the counter (which means that we had obtained a palindrome) and increment the i pointer and decrement the j pointer
2. Consider a situation where the first character doesn't match the last character, then, in this scenario, we will return the maximum of the two values.

We get the maximum value of the string as stated below:

1. Deleting the first character and applying the recursion for the remaining entire string S[i+1,j]
2. Deleting the last character and applying the recursion for the remaining entire string S[i,j-1]

From the above two cases, we are going to pick the maximum value (i.e, maximum palindromic subsequence, which is obtained from the string S).

Time Complexity

For the Naive Approach, the time complexity is going to be as 2^n, as the function call happens for every subroutine.

Note

One thing to be kept in mind is that we should define the base case properly; it may result in a Recursion Depth Exceeded exception.

Recursion calls

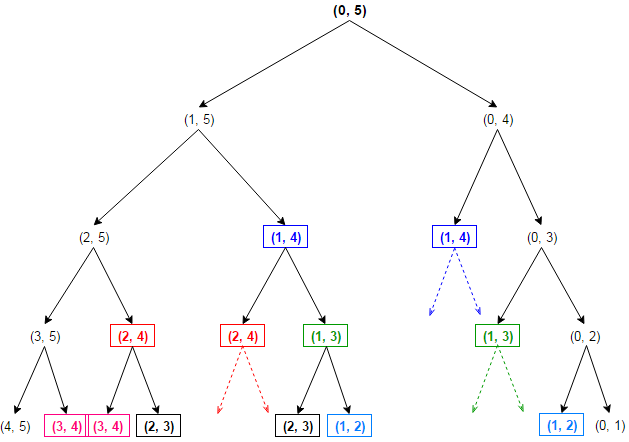
From the above figure, we can understand that recursion has to take place for every subroutine call so this may take a huge time to run and to solve the hierarchical model. This is the main reason why we have the time complexity as 2^n.

Below is the Algorithm Explained

Define a function called longest palindromic subsequence and take two Pointers as i and j and assign them at the 0th position of the string and last posting the string, respectively. Now define the base cases stated below:

Base cases

1. If S[i]==S[j] (this means that, palindrome encountered), then we will return 1.
2. If i > j , this means that if the i pointer exceeds the j pointer, we will simply terminate the process and return 0.

If the S[i] and S[j] are not equal, we will apply the recursion by considering the two possibilities discussed above.

Python Code Using Recursion

# Function to find the Maximum length of the  palindromic subsequence
# of given string
def longestPalindromicsubsequence(S, i, j):

    # Base case
    if i > j: # if i exceeds the  j pointer
        return 0 # stop the flow

    # If the string `S" has only one  Unique char, it is a palindrome
    if i == j:
        return 1 # the maximum length is 1 so we return 1

    # If the last character of the string  matches the  first character
    if S[i] == S[j]:
        # include the first and last characters in palindrome
        # and apply the recursion  for the remaining substring `S[i+1, j-1]`
        return longestPalindromicsubsequence(S, i + 1, j - 1) + 2

    '''
     Consider a situation where the   first character doesn't match the last character, then, in this scenario, we will return the maximum of the two values:

We get the maximum value of the string as stated below:

Deleting the first character and apply the recursion for the remaining  entire string S[i+1,j]
Deleting the last character and apply the recursion for the remaining entire string S[i,j-1]

    '''

    # we will simply Return the maximum of the two possible values
    return max(longestPalindromicsubsequence(S, i, j - 1), longestPalindromicsubsequence(S, i + 1, j))


if __name__ == '__main__': # main function

    S = "ABBDCACB" # input of the string
    n = len(S) # length of the string

    print("The longest palindromic subsequence length  is",
       longestPalindromicsubsequence(S, 0, n - 1))

Output:

'The longest palindromic subsequence length  is', 5

Java Code Using Recursion

public class Main // defining the main class
{
    //defining the function to find  the longest palindromic subsequence
    // of a string of given S
    public static int  longestPalindromicsubsequece(String S, int i, int j)
    {
        // Base case
        if (i > j) {  // if the i pointer  exceeds the j pointer 
            return 0;
        }
 
        // If the string S has only one unique char, it is a palindrome
        if (i == j) {
            return 1;// we will return 1 
        }
 
        // If the first  character of the string  matches the second  character,
        if (S.charAt(i) == S.charAt(j))
        {
            //  then we will include the first and last characters in palindrome
            // and apply recursion  for the remaining substring `S[i+1, j-1]`
            return longestPalindromicsubsequece(S, i + 1, j - 1) + 2;
        }
 
        /*
          If the first character of the string does not match the last character then we will 
            1. Delete  the last character and apply recursion  for the remaining part of the string left
               `S[i, j-1]`
            2. Delete  the first character and apply recursion  for the remaining substring left
               `S[i+1, j]`
        */
 
        return Integer.max( longestPalindromicsubsequece(S, i, j - 1), // we will pick the maximum value
                     longestPalindromicsubsequece(S, i + 1, j));
    }
 
    public static void main(String[] args)
    {
        String S = "ABBDCACB";
        int n = S.length();
 
        System.out.print("The length of the longest palindromic subsequence is "
                +  longestPalindromicsubsequece(S, 0, n - 1));
    }
}

Output:

The length of the longest palindromic subsequence is 5

C++ Version Code Using recursion

#include<bits/stdc++.h>
using namespace std;

// defining a function to return the  max of two integers
int max (int x, int y) { return (x > y)? x : y; }

// Returns the length of the maximum  palindromic subsequence of a given string
int longestpalindromicsubsequence(char *S, int i, int j)
{
// If there is only 1 unique  character then we will return 1
if (i == j) // since it is a palindrome
	return 1;

//2nd base condition, is if there are only two characters present 
if (S[i] == S[j] && i + 1 == j)
	return 2; // then we will return 2  since the length of the the maximum length of the palindromic Subsequence is 2

// If the first and last chars are equal
if (S[i] == S[j])
	return longestpalindromicsubsequence (S, i+1, j-1) + 2;

// If the first char and last char dosentare not equal then we will picj the maximum value
return max( longestpalindromicsubsequence(S, i, j-1), longestpalindromicsubsequence(S, i+1, j) );
}

/* Driver program to test above functions */
int main()
{
	char S[] = "ABBDCACB";
	int n = strlen(S);
	cout << "The length of the Longest  Palindromic Subsequence  is "<< longestpalindromicsubsequence(S, 0, n-1);
	return 0;
}

Output:

The length of the Longest  Palindromic Subsequence  is 5

Approach 2: (Dynamic Programming)

This approach is efficient. Since there exists the optimal overlapping property, we can comfortably implement the Dynamic Programming Approach.

The Main Difference between the Recursion and Dynamic Programming Approach is

In the dynamic programming approach, we will not revisit the computed subroutine, instead, we will save all the computed values in an array and if we encounter the same recursive call to be computed again and again, we will simply make use of the functional value from the table. This approach is called Memoization.

Explanation of Memoization with an example

By Looking at the Figure of recursive calls, we see that while solving the recursive calls (1,5) and (0,4), we get (1,2) as a common recursive call to be computed again and again, so this may consume much more time, to avoid this time consuming, we simply store the value of (1,2) in an array or dictionary. So whenever we again require this value to be computed, we will simply reuse it from the stored array. In this way, we can save a huge amount of time, and we can even reduce the complexity of any algorithm respectively, this is called Dynamic Programming.

Dynamic Programming Algorithm

The Complete Algorithm is the same as the recursive one, and one extra functionality added to this is we will declare an extra key functionality to store pre-computed values.

The complexity of Dynamic programming:

• Time Complexity : O(N^2)
• Space Complexity: O(N^2)

Where N is the length of the Input string.

Note : One thing that is to be kept in mind is that we should define the base case properly else, it may result in Recursion Depth Exceeded the exception.

Python Version Of Dynamic programming

# definition function longestpalandromicstring
def longestpalandromicstring(S, i, j,array):
 
    # Base case 
    if i > j: # if the i pointer exceeds j pointer then we return 0 
        return 0
 
    # If the two pointers are equal means, one unique  character is present 
    if i == j:
        return 1 # then we return 1 
 
    # declaring the key to store the computation calls
    key = (i, j)
 
    # we will check the key, before its computation into the array
    if key not in array: # if it is not present then only we will start the recursion function
 
        
 
        if S[i] == S[j]: # if its matches 
            array[key] = longestpalandromicstring(S, i + 1, j - 1,array) + 2
        else:
            '''      Consider a situation where the   first character doesn't match the last character, then, in this scenario, we will return the maximum of the two values:

We get the maximum value of the string as stated below:

Deleting the first character and apply the recursion for the remaining  entire string S[i+1,j]
Deleting the last character and apply the recursion for the remaining entire string S[i,j-1]
 '''
 
            array[key] = max(longestpalandromicstring(S, i, j - 1, array),
                            longestpalandromicstring(S, i + 1, j, array))
 
    # Return the subproblem solution from the dictionary
    return array[key]
 
 
if __name__ == '__main__':
 
    S = "ABBDCACB"
    n = len(S)
 
    # Create a dictionary to store solutions to subproblems
    array = {}
 
    print("The maximum longest palindromic subsequence is",
        longestpalandromicstring(S, 0, n - 1, array))

Output:

The maximum longest palindromic subsequence is 5

Java Version using Dynamic Programming

import java.util.HashMap;
import java.util.Map;
 // defining the main class
public class Main
{
    
    public static int longestPalindromestring(String S, int i, int j,
                                        Map<String, Integer> map) // defining the longest palindromic string function 
    {// additionally we also declare a hashmap to map the precomputed elements 
        // Base case
        if (i > j) { // if i pointer exceeds the j pointer
            return 0; // we return 0
        }
 
        // If the string `S`contains  only one unique  character, it is a palindrome
        if (i == j) {
            return 1; // we return 1 since a palindrome is found
        }
 
        // we will now built the unique key to map the elements
        String key = i + "|" + j;
 
        // for the first time store  every precomputed value in the map and check for each recursive call
        if (!map.containsKey(key)) // whether it contains the value or not 
        {
            /* If the last character of the string is the same as the first character,
               include the first and last characters in palindrome and recur
               for the remaining substring `X[i+1, j-1]` */
 
            if (S.charAt(i) == S.charAt(j)) { // if the  palindrome is detected, then increment the value by 2
                map.put(key, longestPalindromestring(S, i + 1, j - 1, map )+ 2);
            }
            else {
 
                /*    Consider a situation where the   first character doesn't match the last character, then, in this scenario, we will return the maximum of the two values:

We get the maximum value of the string as stated below:

Deleting the first character and apply the recursion for the remaining  entire string S[i+1,j]
Deleting the last character and apply the recursion for the remaining entire string S[i,j-1]
 */
 
                map.put(key, Integer.max(longestPalindromestring(S, i, j - 1, map), // simply choose the max value
                                            longestPalindromestring(S, i + 1, j, map)));
            }
        }
 
        // Return the precomputed subroutine
        return map.get(key);
    }
 
    public static void main(String[] args)
    {
        String S = "ABBDCACB";
        int n = S.length();
 
        // Create a map to store the precomputed solutions
        Map<String, Integer> array = new HashMap<>();
 
        System.out.print("The maximum longest palindromic subsequence is  " +
                                longestPalindromestring(S, 0, n - 1, array));
    }
}

Output :

The maximum longest palindromic subsequence is  5

C++ Version Using Dynamic Programming

#include <iostream>
#include <string>
#include <unordered_map>
using namespace std;
 
// defining the function to find the maximum longest palindrome subsequence
int longestPalindromestring(string S, int i, int j, auto &map)
{
    // Base condition
    if (i > j) { // if i pointer exceeds j pointer
        return 0; // we will return 0
    }
 
    // If the string string 'S' has only one character, then a palindrome is detected
    if (i == j) {
        return 1; // we will return 1
    }
 
    //we will built a key to store the precomputed values
    string key = to_string(i) + "|" + to_string(j);
 
    // if you encounter the subroutine for the first time then solve it and store it in the map  s we discussed in the above approach
    if (map. find(key) == map. end())
    {
        // if the first and last character are equal, then we will add 2 and increment the i pointer and decrement the j pointer
        if (S[i] == S[j]) 
{
            map[key] = longestPalindromestring(S, i + 1, j - 1, map) + 2;
        }
        else {
 
            /*   Consider a situation where the   first character doesn't match the last character, then, in this scenario, we will return the maximum of the two values:

We get the maximum value of the string as stated below:

Deleting the first character and apply the recursion for the remaining  entire string S[i+1,j]
Deleting the last character and apply the recursion for the remaining entire string S[i,j-1]
 */
 
            map[key] = max (longestPalindromestring(S, i, j - 1, map), // we will simply pick the maximum value
                        longestPalindromestring(S, i + 1, j, map));
        }
    }
 
    //return the subroutine recursive call
    return map[key];
}
 
int main()
{
    string S = "ABBDCACB";
    int n = S.length();
 
    // Create a map to store the subroutine
    unordered_map<string, int> map;
 
    cout << "The length of the longest palindromic subsequence is " <<longestPalindromestring(S, 0, n  1, map);
 
    return 0;
}

Output:

The Maximum Longest Palindromic Subsequence is  5.

Now we will see how to trace and print the Longest Palindromic Subsequence of the given string.

Algorithm

Here, we'll look at how to print the longest palindromic subsequence. The Longest Common Subsequence (LCS) problem is similar to this one. We can solve this problem by using LCS as a subroutine. The LCS-based two-step solution is shown below. 1) Reverse the given sequence and save it in a new array called rev[0..n-1]. 2) The given sequence's LCS and rev[] will be the palindromic series that is the longest. 3) Once we've located LCS, we can print it.

Below is the Approach

Python version Dynamic programming

# The LCS problem is implemented using dynamic programming.

# Returns the LCS length for STRING1[0..m-1], STRING2[0..n-1], and STRING2[0..n-1].
def lcs(X, Y, m, n):
	array = [[0 for x in range(n+1)] for x in range(m+1)]

#Construct the array [m+1][n+1] from the bottom up using the steps below.
	for i in range(m+1):
		for j in range(n+1):
			if i == 0 or j == 0:
				array[i][j] = 0
			elif string1[i-1] == string2[j-1]:
				array[i][j] = array[i-1][j-1] + 1
			else:
				array[i][j] = max(array[i-1][j], array[i][j-1])

# To print LCS, use the code below.
	index = array[m][n]

	# To store the lcs string, construct a character list.
	lcs = [""] * (index+1)
	lcs[index] = ""

	#Begin at the right-most-bottom-most corner and 
	#store characters in lcs[] one by one.
	j = n
	while i > 0 and j > 0:

	#If the current character in X[] and Y[] is the same, then the current character belongs to LCS.
		if string1[i-1] == string2[j-1]:
			lcs[index-1] = string1[i-1]
			i-=1
			j-=1
			index-=1

	#If the values are not equal, find the larger of the two and proceed in the direction of the larger value.
		elif array[i-1][j] > array[i][j-1]:
			i-=1
		else:
			j-=1

	print("LCS of " + string1 + " and " + string2 + " is " + "".join(lcs))

# Driver program
string1 = "ABBDCACB"
string2 = 'BCACDBBA' # reverse of string1
m = len(string1)
n = len(string2)
lcs(string1, string2, m, n)

Output:

LCS of ABBDCACB and BCACDBBA is BCACB

Java Version of Dynamic Programming

 // defining the Function to print longest palindromic subsequence of string `string1[0…m-1]` and `string2[0…n-1]`
public class  palindromicsubsequence { 
  
 /* LCS string1 and string2 are returned */
    static String lcs(String string1, String string2) { 
        int m = string1.length(); 
        int n = string2.length(); 
        char X1[] = string1.toCharArray(); 
        char Y1[] = string2.toCharArray(); 
  
        int table[][] = new int[m + 1][n + 1]; 
  
/* Construct table[m+1][n+1] from the bottom up using the steps below. Table[i][j] includes the lengths of string1[0..i-1] and string2[0..j-1] LCS. */

        for (int i = 0; i <= m; i++) { 
            for (int j = 0; j <= n; j++) { if (i == 0 || j == 0) { table[i][j] = 0; } else if (X1[i - 1] == Y1[j - 1]) { table[i][j] = table[i - 1][j - 1] + 1; } else { table[i][j] = Math.max(table[i - 1][j], table[i][j - 1]); } } } // To print LCS, use the code below. int pointer = table[m][n]; // Make a String of index+1 length and fill it with it char[] lcstore = new char[pointer + 1]; // Begin at the right-most-bottom-most / corner and store characters in lcstore[] one after the other. int i = m, j = n; while (i > 0 && j > 0) { 
           //If the current character in string1[] and string2 are the same, then the current character is part of the LCStore.
            if (X1[i - 1] == Y1[j - 1]) { 
                // insert the  character in result  
                lcstore[pointer - 1] = X1[i - 1]; 
                i--; 
                j--; 
  
                // decrement the  of i, j and pointer  values
                pointer--; 
            } //If the two values are not equal, find the larger of the two and proceed in the direction of the larger / value.
            else if (table[i - 1][j] > table[i][j - 1]) { 
                i--; 
            } else { 
                j--; 
            } 
        } 
        String answer = ""; 
        for (int x = 0; x < lcstore.length; x++) { answer += lcstore[x]; } return answer; } // Returns str's longest palindromic subsequence. static String lps(String str2) { //Find the opposite of str. String rev = str2; rev = reverse(rev); // Return the LCS of str as well as its inverse. return lcs(str2, rev); } static String reverse(String str3) { String answer = ""; //toCharArray() converts a String to a character array. char[] try1 = str3.toCharArray(); for (int i = try1.length - 1; i >= 0; i--) { 
            answer += try1[i]; 
        } 
        return answer; 
    } 
  
/* Test driver programme for the above identified feature */
    public static void main(String[] args) { 
        String str1 = "ABBDCACB"; 
        System.out.println(lps(str1)); 
  
    } 
} 

C++ Version Of Dynamic Programming

/* c++ program to trace the longest palindromic subsequence */
#include<bits/stdc++.h>
using namespace std;

/* Returns LCS of string1 and string2 */
string  longestcommonsubsequence(string &string1, string &string2)
{
	int m = string1.length();
	int n = string2.length();

	int table[m+1][n+1];

/* In the following steps, construct the table [m+1][n+1] in a bottom-up fashion. It is worth noting that table[i][j] contains the length of LCS for strings1[0..i-1] and string2[0..j-1]. */
	for (int i=0; i<=m; i++)
	{
		for (int j=0; j<=n; j++) { if (i == 0 || j == 0) table[i][j] = 0; else if (string1[i-1] == string2[j-1]) table[i][j] = table[i-1][j-1] + 1; else table[i][j] = max(table[i-1][j], table[i][j-1]); } } // The code below is used to print LCS. int index1 = table[m][n]; // Make a string of index+1 length and assign all zeros to string lcsequence(index+1, '0'); string longestcommonsubsequence(index1+1, '\0'); int i = m, j = n; while (i > 0 && j > 0)
	{
			// If current character in string1[] and string2 are same, then current character ti is said that,it  is the  part of LCS
		if (string1[i-1] == string2[j-1])
		{
		// insert the current char into the result
			longestcommonsubsequence[index1-1] = string1[i-1];
			i--;
			j--;

		// start reducing the values i,j,index
			index1--;
		}

		
		// if they are not same then find the largest of them
		else if (table[i-1][j] > table[i][j-1])
			i--;
		else
			j--;
	}

	return  longestcommonsubsequence;
}


// this function returns the longest palindromic subsequence

string lps(string &str1)
{
	// reverse of the given input string is found
	string rev = str1;
	reverse(rev.begin(), rev.end());

// we will now return the reverse of the string
	return longestcommonsubsequence(str1, rev);
}

// Driver code
int main()
{
	string str1 = "ABBDCACB";
	cout << lps(str1);
	return 0;
}

Conclusion

1. In the above article, we have learned the following basic things:
   1. What is a subsequence?
   2. What is an optimal substructure?
   3. What is the overlapping subproblem property?
2. We have also learned about the detailed procedure to solve the Longest palindromic subsequence along with its path.
3. We did so using the Naive Approach and the Dynamic Programming Approach.

We hope that you will now be able to solve this problem, as well as its variants, without any difficulty.

People are also reading:

• Depth First Search(DFS)- DSA
• Merge Two Sorted Arrays in-place
• Queue Data Structure
• Print all subarrays with 0 sum
• Pattern Program in C
• Rearrange an array in maximum minimum form
• Longest subarray with sum as K
• Find whether an array is subset of another array
• Rod Cutting Problem – Dynamic Programming
• Print a given matrix in spiral form
• Program to Rotate an Array