Check if a Binary Tree is Height-Balanced or Not

Problem

Given a binary tree. You need to check if it is height-balanced or not. A tree is height-balanced if the absolute difference between the height of the left and right subtrees is not more than 1.

Sample Input

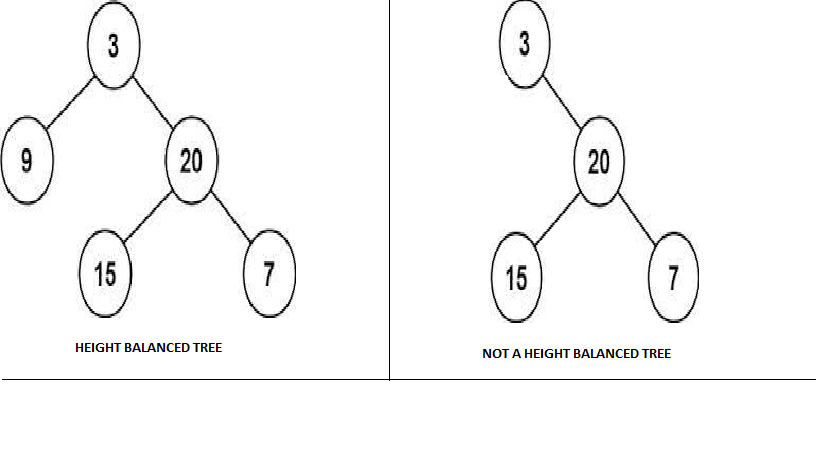
Sample Output

YES

Explanation

Each node’s left and right subtree difference does not exceed 1.

Approach

We can use DFS to solve this problem. We go to the depth of the tree (leaf nodes) and keep returning heights to the parent nodes. The height returned by a child to its parent would be 1 greater than the maximum height of this child. This way, we keep track of the height difference of each node’s subtrees. The child returns height to its parent when we backtrack. For instance, if the tree is

             1
          /     \
         2       3

1 -> 2 -> NULL, NULL returns 0 2 -> NULL, NULL returns 0 (Now backtrack and return 1+max(2->left, 2->right)) 1 will now have height of its left subtree as 1 1 -> 3 -> NULL, NULL returns 0 3 -> NULL, NULL returns 0 (Now backtrack and return 1+max(3->left, 3->right)) 1 will now have height of its right subtree as 1 The absolute difference would be 1-1=0 which is height-balanced.

Complexity Analysis

The time complexity would be O(N), and the space complexity would also be O(N) due to the call stack.

C++ Programming

#include<bits/stdc++.h>
using namespace std;

struct TreeNode
{
    int val;
    TreeNode *left, *right;

    TreeNode(int val)
    {
        this->val = val;
        this->left = this->right = nullptr;
    }
};

int dfs(TreeNode* root, bool &ok)
{
    // if NULL node found
    if (root == nullptr || !ok) {
        return 0;
    }

    // get the height of the left subtree
    int left = dfs(root->left, ok);

    // get the height of the right subtree
    int right = dfs(root->right, ok);

    if (abs(left - right) > 1) {
        ok = false;
    }

    // return height of subtree rooted at the current node
    return max(left, right) + 1;
}

bool dfs(TreeNode* root)
{
    bool ok = true;
    dfs(root, ok);
    return ok;
}

int main()
{
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);

    if (dfs(root)) {
        cout << "Tree is balanced";
    }

    else {
        cout << "Tree is not balanced";
    }
    return 0;
}

Output

Tree is balanced

Java Programming

import java.util.concurrent.atomic.AtomicBoolean;

class TreeNode
{
    int val;
    TreeNode left = null, right = null;

    TreeNode(int val) {
        this.val = val;
    }
}

class Main
{
    public static int dfs(TreeNode root, AtomicBoolean ok)
    {
        // if node is NULL
        if (root == null || !ok.get()) {
            return 0;
        }
        // left subtree height 
        int left = dfs(root.left, ok);

        // right subtree height
        int right = dfs(root.right, ok);

        if (Math.abs(left - right) > 1) {
            ok.set(false);
        }

        // return height of subtree rooted at the current node
        return Math.max(left, right) + 1;
    }

    public static boolean dfs(TreeNode root)
    {
        AtomicBoolean ok = new AtomicBoolean(true);
        dfs(root, ok);
        return ok.get();
    }

    public static void main(String[] args)
    {
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);

        if (dfs(root)) {
            System.out.print("Tree is balanced");
        }

        else {
            System.out.print("Tree is not balanced");
        }
    }
}

Output

Tree is balanced

Python Programming

class TreeNode:
    def __init__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def dfs(root, ok=True):
    # if node is NULL
    if root is None or not ok:
        return 0, ok

    # get the height of the left subtree
    left, ok = dfs(root.left, ok)

    # get the height of the right subtree
    right, ok = dfs(root.right, ok)

    if abs(left - right) > 1:
        ok = False

    # return height too parent
    return max(left, right) + 1, ok

root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)

if dfs(root)[1]:
    print("Tree is balanced")
else:
    print("Tree is not balanced")

Output

Tree is balanced

People are also reading:

• Merge Two Sorted Arrays in-place
• Subarray with Sum k
• Longest Palindromic Subsequence using Dynamic Programming
• Maximum Sum Circular Subarray
• Find Maximum Subarray Sum
• Sort an array in one swap whose two elements are swapped
• Dutch National Flag Problem
• Construct a tree from Inorder and Level order traversals
• Rearrange an array such that arr[i] = i
• Minimum Edit Distance