You are given a Binary Tree. Your task is to convert it into a doubly-linked list. The left and right child of the nodes of the Binary Tree is to be converted into previous and next pointers of the linked list, respectively. Nodes of the doubly linked list must be according to the inorder of the binary tree. The leftmost node or the first node of the inorder of the tree will be the head of the tree.
Approach 1
In this approach, we will traverse the tree twice: first for fixing the left pointer and again for fixing the right pointer.
Fixing the left pointer: This is the first step of this approach. We will iterate through the tree in an inorder fashion and will keep track of the previously visited node so that we can change the left pointer to the previous node.
Fixing the right pointer: This is complex as compared to the previous step. We will be using the left pointers fixed in step one. Since the right-most node is the last node of the doubly linked list, we will start from there. We will traverse the tree linearly as the left pointers are already pointing to the previous nodes. We will keep track of the previously visited node and change the right pointer to the previous node during traversal.
Algorithm
- Create a node with the value being set as the data that is passed as the parameter and initialize its left and right children to NULL.
- Traverse the binary tree in inorder traversal while updating the previous pointers in the list, with the left child nodes.
- Traverse the binary tree in inorder traversal while updating the next pointers in the list with the right child nodes.
- Traverse the tree and get the DLL's last node, or the node at the farthest right side of the tree
- Now, for updating the right pointers by traversing backward from the farthest right node with the help of the left nodes.
- Traverse over the doubly linked list from the left node to the right node to print it.
The implementation of the above-discussed approach is:
CPP
#include <bits/stdc++.h>
using namespace std;
// Class for a node
// having an integer value, data
// and two pointers
// to store the references of the
// left and right children
class node
{
public:
int data;
node *left, *right;
};
// function to create a node
// with the value being set as the data
// that is passed as the parameter,
// and initializing its left and right children to NULL
node *newNode(int data)
{
node *Node = new node();
Node->data = data;
Node->left = Node->right = NULL;
return(Node);
}
// function to traverse tree in an
// inorder fashion
void inorder(node *root)
{
if (root != NULL)
{
inorder(root->left);
cout << " " << root->data;
inorder(root->right);
}
}
// function to traverse the binary tree
// in inorder traversal, while
// updating the previous pointers
// in the list, with the left child nodes.
void setPrevPtr(node *root)
{
static node *pre = NULL;
if (root != NULL)
{
setPrevPtr(root->left);
root->left = pre;
pre = root;
setPrevPtr(root->right);
}
}
// function to traverse the binary tree
// in inorder traversal, while
// updating the next pointers
// in the list, with the right child nodes.
node *setNextPtr(node *root)
{
node *prev = NULL;
// to traverse the tree and
// get the DLL's last node, or
// the node at farthest right side
// in the tree
while (root && root->right != NULL)
root = root->right;
// now, for updating the right pointers
// by traversing backwards,
// from the farthest right node
// with the help of the left nodes.
while (root && root->left != NULL)
{
prev = root;
root = root->left;
root->right = prev;
}
// return the head of the linked list
// i.e., the node at the farthest left side.
return (root);
}
// function to transform the binary tree
// into doubly linked lists.
node *convertBT(node *root)
{
// for the setting of the previous pointer
setPrevPtr(root);
// for the setting of the next pointer
return setNextPtr(root);
}
// to print, traverse over the doubly linked list
// from the left node to the right node.
void printDLL(node *root)
{
while (root != NULL)
{
cout<<" "<data;
root = root->right;
}
}
// Driver code
int main(void)
{
node *root = newNode(10);
root->left = newNode(12);
root->right = newNode(15);
root->left->left = newNode(25);
root->left->right = newNode(30);
root->right->left = newNode(36);
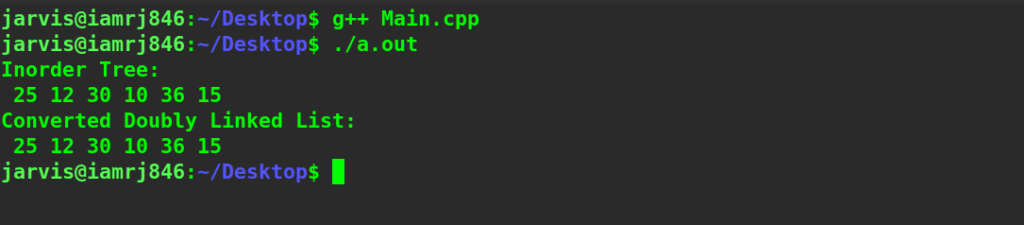
cout<<"Inorder Tree:\n";
inorder(root);
node *head = convertBT(root);
cout << "\nConverted Doubly Linked List:\n";
printDLL(head);
return 0;
}
Output
Inorder Tree: 25 12 30 10 36 15 Converted Doubly Linked List: 25 12 30 10 36 15
JAVA
public class ConvertBT
{
static class node
{
int data;
node left, right;
public node(int data)
{
this.data = data;
}
}
static node prev;
// function to traverse the binary tree
// in inorder traversal, while
// updating the previous pointers
// in the list, with the left child nodes.
static void setPrevPtr(node root)
{
if (root == null)
return;
setPrevPtr(root.left);
root.left = prev;
prev = root;
setPrevPtr(root.right);
}
// function to traverse the binary tree
// in inorder traversal, while
// updating the next pointers
// in the list, with the right child nodes.
static node setNextPtr(node root)
{
// to traverse the tree and
// get the DLL's last node, or
// the node at farthest right side
// in the tree
while (root.right != null)
root = root.right;
// now, to updating the right pointers
// by traversing backwards,
// from the farthest right node
// with the help of the left nodes.
while (root != null && root.left != null)
{
node left = root.left;
left.right = root;
root = root.left;
}
// return the head of the linked list
// i.e., the node at the farthest left side.
return root;
}
// method to transform the binary tree
// into doubly linked list.
static node BTTtoDLL(node root)
{
prev = null;
// for the setting of the previous pointer
setPrevPtr(root);
// for the setting of the next pointer
return setNextPtr(root);
}
// to print, traverse over the doubly linked list
// from the left node to the right node.
static void printDLL(node root)
{
while (root != null)
{
System.out.print(" ");
System.out.print(root.data + " ");
root = root.right;
}
}
// function to traverse tree in an
// inorder fashion
static void inorder(node root)
{
if (root == null)
return;
inorder(root.left);
System.out.print(" ");
System.out.print(root.data + " ");
inorder(root.right);
}
public static void main(String[] args)
{
node root = new node(10);
root.left = new node(12);
root.right = new node(15);
root.left.left = new node(25);
root.left.right = new node(30);
root.right.left = new node(36);
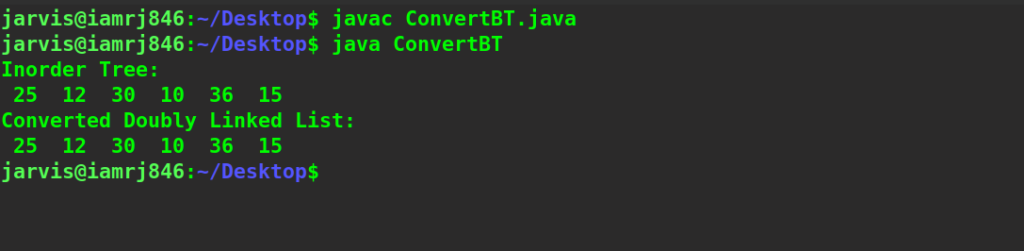
System.out.println("Inorder Tree:");
inorder(root);
node head = BTTtoDLL(root);
System.out.println("\nConverted Doubly Linked List:");
printDLL(head);
}
}
Output
Inorder Tree: 25 12 30 10 36 15 Converted Doubly Linked List: 25 12 30 10 36 15
Python
# Class for a node
# having an integer value, data
# and two pointers
# to store the references of the
# left and right children
class Node:
# constructor to create a node
# with the value being set as the data
# that is passed as the parameter,
# and initializing its left and right children to NULL
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# function to traverse tree in an
# inorder fashion
def inorder(root):
if root is not None:
inorder(root.left)
print (" %d" %(root.data))
inorder(root.right)
# function to traverse the binary tree
# in inorder traversal, while
# updating the previous pointers
# in the list, with the left child nodes.
def setPrevPtr(root):
if root is not None:
setPrevPtr(root.left)
root.left = setPrevPtr.pre
setPrevPtr.pre = root
setPrevPtr(root.right)
# function to traverse the binary tree
# in inorder traversal, while
# updating the next pointers
# in the list, with the right child nodes.
def setnextPtr(root):
prev = None
# to traverse the tree and
# get the DLL's last node, or
# the node at farthest right side
# in the tree
while(root and root.right != None):
root = root.right
# now, to updating the right pointers
# by traversing backwards,
# from the farthest right node
# with the help of the left nodes.
while(root and root.left != None):
prev = root
root = root.left
root.right = prev
# return the head of the linked list
# i.e., the node at the farthest left side.
return root
# function to transform the binary tree
# into a doubly linked list.
def ConvertBT(root):
# for the setting of the previous pointer
setPrevPtr(root)
# for the setting of the next pointer
return setnextPtr(root)
# to print, traverse over the doubly linked list
# from the left node to the right node.
def printDLL(root):
while(root != None):
print (" %d" %(root.data))
root = root.right
# Driver program to test above function
root = Node(10)
root.left = Node(12)
root.right = Node(15)
root.left.left = Node(25)
root.left.right = Node(30)
root.right.left = Node(36)
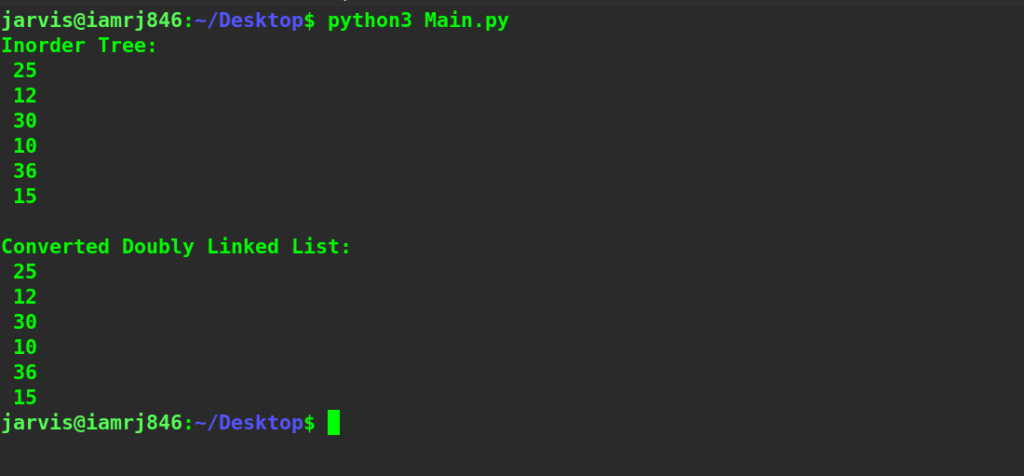
print ("Inorder Tree:")
inorder(root)
setPrevPtr.pre = None
head = ConvertBT(root)
print ("\nConverted Doubly Linked List:")
printDLL(head)
Output
Inorder Tree: 25 12 30 10 36 15 Converted Doubly Linked List: 25 12 30 10 36 15
Time Complexity: O(n), where n is the number of nodes. Because we are simply traversing the tree twice in the inorder fashion.
Approach 2
This approach is simpler than the previous one. In this approach, we will iterate over the tree in the inorder fashion and keep a track of the node that has been traversed, let’s say prev. Now, for every visited node, update it as the next of prev and previous of this node as prev .
Algorithm
- Recursively convert the binary tree whose root has been passed to it as a parameter to a doubly linked list, whose head has also been passed to it as a parameter.
- Convert recursively the right subtree into dll.
- Place the root of the binary tree into the doubly linked list.
- Update the previous head using the left pointer
- Update the dll's head
- Print, traverse over the doubly linked list.
- Convert recursively the right subtree into dll.
- From the left node to the right node.
- Traverse from left node to right node to print.
The implementation of the above-discussed approach is:
CPP
`#include <bits/stdc++.h>
using namespace std;
// Structure for a node and tree
// having an integer value, data
// and two pointers
// to store the references of the
// left and right children
struct Node {
int data;
Node *left, *right;
};
// function to create a node
// with the value being set as the data
// that is passed as the parameter,
// and initializing its left and right children to NULL
Node* newNode(int data)
{
Node* node = new Node;
node->data = data;
node->left = node->right = NULL;
return node;
}
// function to recursively convert the binary tree
// whose root has been passed to it as a parameter
// to a doubly-linked list, whose head has also been passed
// to it as a parameter.
void ConvertBT(Node* root, Node*& head)
{
// Base cases
if (root == NULL)
return;
// convert recursively the right subtree
// into dll.
ConvertBT(root->right, head);
// placing the root of the
// binary tree into the
// doubly linked list.
root->right = head;
// updating the previous head
// using the left pointer
if (head != NULL)
head->left = root;
// updating the dll's head
head = root;
// convert recursively the left subtree
// into dll.
ConvertBT(root->left, head);
}
// to print, traverse over the doubly linked list
// from the left node to the right node.
void printDLL(Node* head)
{
cout << "Converted Doubly Linked List:\n";
while (head) {
cout << " " << head->data;
head = head->right;
}
}
int main()
{
Node *root = newNode(10);
root->left = newNode(12);
root->right = newNode(15);
root->left->left = newNode(25);
root->left->right = newNode(30);
root->right->left = newNode(36);
Node* head = NULL;
ConvertBT(root, head);
printDLL(head);
return 0;
}
Output
Converted Doubly Linked List: 25 12 30 10 36 15

JAVA
// class for a node and tree
// having an integer value, data
// and two pointers
// to store the references of the
// left and right children
class Node {
int data;
Node left, right;
public Node(int data)
{
this.data = data;
left = right = null;
}
}
class BinaryTree {
Node root;
Node head;
// function to recursively convert the binary tree
// whose root has been passed to it as a parameter
// to a doubly linked list, whose head as also been passed
// to it as a parameter.
void ConverBT(Node root)
{
// Base cases
if (root == null)
return;
// convert recursively the right subtree
// into dll
ConverBT(root.right);
// placing the root of the
// binary tree into the
// doubly linked list.
root.right = head;
// updating the previous head
// using the left pointer
if (head != null)
head.left = root;
// updating the dll's head
head = root;
// convert recursively the left subtree
// into dll.
ConverBT(root.left);
}
// to print, traverse over the doubly lined list
// from the left node to the right node.
void printDLL(Node head)
{
System.out.println("Converted Doubly Linked List:");
while (head != null) {
System.out.print(head.data + " ");
head = head.right;
}
}
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(10);
tree.root.left = new Node(12);
tree.root.right = new Node(15);
tree.root.left.left = new Node(25);
tree.root.left.right = new Node(30);
tree.root.right.left = new Node(36);
tree.ConverBT(tree.root);
tree.printDLL(tree.head);
}
}
Output
Converted Doubly Linked List: 25 12 30 10 36 15

Python
# class for a node and tree
# having an integer value, data
# and two pointers
# to store the references of the
# left and right children
class Node:
def __init__(self, data):
self.data = data
self.left = self.right = None
class BinaryTree:
# function to recursively convert the binary tree
# whose root has been passed to it as a parameter
# to a doubly linked list, whose head as also been passed
# to it as a parameter.
root, head = None, None
def ConvertBT(self, root: Node):
if root is None:
return
# convert recursively the right subtree
# into dll
self.ConvertBT(root.right)
# placing the root of the
# binary tree into the
# doubly linked list.
root.right = self.head
# updating the previous head
# using the left pointer
if self.head is not None:
self.head.left = root
# updating the dll's head
self.head = root
# convert recursively the left subtree
# into dll
self.ConvertBT(root.left)
def printDLL(self, head: Node):
print('Converted Doubly Linked List:')
while head is not None:
print(head.data, end = ' ')
head = head.right
if __name__ == '__main__':
tree = BinaryTree()
tree.root = Node(10)
tree.root.left = Node(12)
tree.root.right = Node(15)
tree.root.left.left = Node(25)
tree.root.left.right = Node(30)
tree.root.right.left = Node(36)
tree.ConvertBT(tree.root)
tree.printDLL(tree.head)
Output
Converted Doubly Linked List: 25 12 30 10 36 15

Time Complexity: O(n), where n is the number of nodes. Because we are simply applying the inorder traversal.
Approach 3
The basic idea of this approach is that we perform the inorder traversal over the tree. Add nodes at the starting of the current linked list and update the head of the list. Because we are adding the node at the start, we have to operate leaf nodes in the reverse order.
Algorithm
- Create a static variable to store the node visited previously.
- Convert recursively the left subtree into dll.
- Convert recursively the right subtree into dll.
- Traverse over the doubly linked lis from the left node to the right node to print.
The implementation of the above-discussed approach is
CPP
#include
using namespace std;
// Structure for a node
// having an integer value, data
// and two pointers
// to store the references of the
// left and right children
struct node
{
int data;
node* left;
node* right;
};
// function to recursively convert the binary tree
// whose root has been passed to it as a parameter
// to a doubly-linked list, whose head as also been passed
// to it as a parameter.
void ConvertBT(node *root, node **head)
{
// Base case
if (root == NULL) return;
// static variable to
// store the node visited previously.
// initialize it to null
static node* prev = NULL;
// convert recursively the left subtree
// into dll.
ConvertBT(root->left, head);
if (prev == NULL)
*head = root;
else
{
root->left = prev;
prev->right = root;
}
prev = root;
// convert recursively the right subtree
// into dll.
ConvertBT(root->right, head);
}
// function to create a node
// with the value being set as the data
// that is passed as the parameter,
// and initializing its left and right children to NULL
node* newNode(int data)
{
node* new_node = new node;
new_node->data = data;
new_node->left = new_node->right = NULL;
return (new_node);
}
// to print, traverse over the doubly linked list
// from the left node to the right node.
void printDLL(node *node)
{
while (node!=NULL)
{
cout << node->data << " "; node = node->right;
}
}
int main()
{
node *root = newNode(10);
root->left = newNode(12);
root->right = newNode(15);
root->left->left = newNode(25);
root->left->right = newNode(30);
root->right->left = newNode(36);
node *head = NULL;
ConvertBT(root, &head);
cout << "\nConverted Doubly Linked List:\n";
printDLL(head);
return 0;
}
Output
Converted Doubly Linked List: 25 12 30 10 36 15

JAVA
// Class for a node
// having an integer value, data
// and two pointers
// to store the references of the
// left and right children
class Node
{
int data;
Node left, right;
public Node(int data)
{
this.data = data;
left = right = null;
}
}
class BinaryTree
{
Node root;
Node head;
// static variable to
// store the node visited previously.
// initialize it to null
static Node prev = null;
// function to recursively convert the binary tree
// whose root has been passed to it as a parameter
// to a doubly linked list, whose head as also been passed
// to it as a parameter.
void ConvertBT(Node root)
{
// Base case
if (root == null)
return;
// convert recursively the left subtree
// into dll.
ConvertBT(root.left);
if (prev == null)
head = root;
else
{
root.left = prev;
prev.right = root;
}
prev = root;
// convert recursively the right subtree
// into dll.
ConvertBT(root.right);
}
// to print, traverse over the doubly linked list
// from the left node to the right node.
void printDLL(Node node)
{
while (node != null)
{
System.out.print(node.data + " ");
node = node.right;
}
}
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(10);
tree.root.left = new Node(12);
tree.root.right = new Node(15);
tree.root.left.left = new Node(25);
tree.root.left.right = new Node(30);
tree.root.right.left = new Node(36);
tree.ConvertBT(tree.root);
System.out.println("\nConverted Doubly Linked List:");
tree.printDLL(tree.head);
}
}
Output
Converted Doubly Linked List: 25 12 30 10 36 15

Python
class Node:
def __init__(self, val):
self.right = None
self.data = val
self.left = None
class BtoDll:
def __init__(self):
self.head = None
self.tail = None
def convert(self, root):
# Base case
if root is None:
return
# convert recursively the left subtree
# into dll.
self.convert(root.left)
node = root
if self.head is None:
self.head = node
else:
self.tail.right = node
node.left = self.tail
self.tail = node
# convert recursively the right subtree
# into dll.
self.convert(root.right)
return self.head
def ConvertBT(root):
# function to recursively convert the binary tree
# whose root has been passed to it as a parameter
# to a doubly linked list, whose head as also been passed
# to it as a parameter.
converter = BtoDll()
return converter.convert(root)
def printDLL(head):
# to print, traverse over the doubly linked list
# from the left node to the right node.
while head is not None:
print(head.data, end=" ")
head = head.right
if __name__ == "__main__":
root = Node(10)
root.left = Node(12)
root.right = Node(15)
root.left.left = Node(25)
root.left.right = Node(30)
root.right.left = Node(36)
head = ConvertBT(root)
print("Converted Doubly Linked List:")
printDLL(head)
Output
Converted Doubly Linked List: 25 12 30 10 36 15
Time Complexity:
O(n), where n is the number of nodes, as we are applying simple in order traversal.

Wrapping Up!
In this article, we have learned an amazing concept of Binary Trees. Binary Tree is one of the most important data structures and is usually asked in the top interview questions as well. “Convert a Binary Tree into a doubly-linked list” is a popular as well as a very important problem that has been asked in various interview questions. We also covered in detail how all the three approaches work and what are the significance of them respectively. We discussed their time complexity as well as space complexity along with a proper explanation. Different programmers prefer different languages for coding. So, we made sure that all our readers can refer to this article. That’s why, this article also contains well-explained codes for all the three approaches in the three most popular languages which are c++, Java, and python along with their respective outputs attached to the article for a better understanding of a wide range of our readers. We sincerely hope that this article has walked you through some deep and important concepts of Binary Trees and how we should approach such kinds of problems. We surely wish you to keep up your practice and crack all the questions easily. With this, we are wrapping up this article. Happy Learning! People are also reading:
- What is Shell Sort?
- How to find and remove loops in a Linked List?
- WAP in C++ & Python to find the largest & smallest element in Array
- Difference Between Repeater, DataList and GridView
- Circular Linked List
- What is Structured Programming?
- Tree vs Graph
- DSA: Binary Heap Tree
- Asymptotic Analysis
- Fibonacci Series





Leave a Comment on this Post