There are a plethora of sorting algorithms present for arrays like the bubble sort, insertion sort, selection sort, heap sort, merge sort, quick sort, and many more. But in the case of Linked Lists, the implementation of all the sorting algorithms is difficult. Heapsort is totally impossible for sorting the linked list.
In this article, we will discuss how to apply the Merge Sort algorithm to sort the given linked list in ascending order.
Given a singly linked list containing n number of nodes, sort the linked list in the ascending order using the merge sort sorting algorithm.

Inputs:
- 11-> 2 -> 4 -> 1 -> 9-> null
- 1 -> null
Outputs:
- 1 -> 2 -> 4 -> 9 -> 11 -> null
- 1 -> null
Merge Sort Algorithm for Array’s data structure
- Check for the condition start<end.
- First of all, find the middle element of the array. Middle element is equal to the(start+(end-start)/2).
- Recursively call the array for 0(start) to mid element(end) and mid+1(start) to length-1 of the array until start < end .
- Call MergeSort (start ,mid ,end).
- In MergeSort Function, sort the two halves for the array.
The above algorithm is not suitable for the Linked List sorting because, in Linked List, we cannot access a particular node of the linked list in O(1). This is because of the non-contiguous memory allocation of the Linked List.
On the other hand, arrays have contiguous memory allocation. We can easily find the middle element but in the case of the linked list, we have to use another algorithm i.e the Tortoise-Hare Algorithm.
TORTOISE-HARE Algorithm
- Iterate the Linked List using two pointers/references, one pointer is slow and the other pointer/reference is fast.
- Update the slow pointer/reference by one node and the fast pointer/reference by two nodes.
- Return the slow pointer/reference which is the middle node of the linked list.
The rest of the steps to perform the merge sort in the linked list are the same with very few variations.
Approach
- Find the middle element of the Linked List using the TORTOISE-HARE algorithm.
- Divide the element into two halves head and middle.next position of the linked list.
- Recursively Divide the generated halves into another half till head or head.next becomes null.
- Merge the two halves by sorting each node’s data.
JAVA
//Importing Libraries
import java.util.*;
import java.io.*;
//Creating class Node
class Node{
int data; //Creating data element to be stored in the node of the linked list
Node next;//Creating next reference of the node in the linked list
//Creating Constructor to initialize the data members
public Node(int data){
this.data=data;
this.next=null;
}
}
//Creating MergeLinkedList class
class MergeLinkedList{
static Node head;//Creating head reference of the linked list
//Creating function to push the node a
static void push(int data){
//Checking the base condition
if(head==null){
//Creating head of the linked list
head=new Node(data);
}
else{
//Creating temporary reference of the head
Node temp=head;
//Iterate the linked list
while(temp.next!=null){
temp=temp.next;
}
//insert the node at the end of the linked list
temp.next=new Node(data);
}
}
//Function to print the linked list
static void print(Node head){
//Iterate the head of the linked list
while(head!=null){
//Print the node value of the linked list
System.out.print(head.data+" ");
//Update the head of the linked list
head=head.next;
}
}
//Function to get the middle element of the given linked list
static Node Middle Element(Node head){
//Checking the base condition
if(head==null){
//Return the head if the head is null
return head;
}
//Creating two reference for the linked list
//Slow Reference
Node slow=head;
//Fast Reference
Node fast=head;
//Iterate the Linked list using fast reference of the linked list
while(fast.next!=null && fast.next.next!=null){
//Update the slow pointer
slow=slow.next;
//Update the fast pointer
fast=fast.next.next;
}
//Return the slow reference that contains the middle element of the linked list
return slow;
}
//Function to sort the two halves of the linked list
static Node sortedMerge(Node left,Node right){
//Checking the base conditions
if(left==null){
return right;
}
if(right==null){
return left;
}
//Creating a temporary reference to refer to to the sorted linked list
Node result=null;
//Checking if the left reference data is smaller than the right reference data
if(left.data<=right.data){
//Update the result reference
result=left;
//Recursively call the left.next for next node
result.next=sortedMerge(left.next, right);
}
else{
//Update the result reference
result=right;
//Recursively call the left.next for next node
result.next=sortedMerge(left, right.next);
}
//Return the sorted linked list
return result;
}
//Function to perform the merge sort of the linked list
static Node mergeSort(Node head){
//Checking the base conditions
if(head==null||head.next==null){
return head;
}
//Getting the middle element
Node firsthalf=Middleelement(head);
//Creating second half of the linked list
Node secondHalf=firsthalf.next;
//Break the middle element reference
firsthalf.next=null;
//Recursively call the two halves of the linked list
Node left=mergeSort(head);
Node right=mergeSort(secondHalf);
//call for the sorting
Node sortedList=sortedMerge(left,right);
//Return the complete sorting linked list
return sortedList;
}
public static void main(String[] args) {
//Creating object of merge linked list
MergeLinkedList ob =new MergeLinkedList();
//Creating first node of the linked list
ob.push(15);
//Creating second node of the linked list
ob.push(10);
//Creating third node of the linked list
ob.push(5);
//Creating fourth node of the linked list
ob.push(20);
//Creating fifth node of the linked list
ob.push(3);
//Creating sixth node of the linked list
ob.push(2);
//Printing original linked list
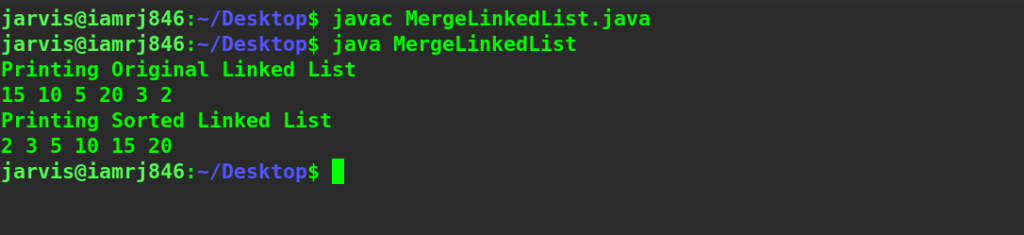
System.out.println("Printing Original Linked List");
ob.print(head);
//Creating new line
System.out.println();
//Call for sorting the linked list
ob.head=mergeSort(ob.head);
//Printing the sorted linked list
System.out.println("Printing Sorted Linked List");
ob.print(head);
}
}
Output:
Python
#Creating Node class
class Node:
def __init__(self,data):
self.data=data #Creating data of the node
self.next=None #Creating next reference of the node of the linked list
#Creating Linked List
class LinkedList:
#Creating Linked List class constructor
def __init__(self):
self.head=None
#Function to push the node in the linked list
def push(self,data):
#Checking the base condition
if(self.head is None):
#Creating First node of the linked list
self.head=Node(data)
else:
#Creating temporary reference of the linked list
temp=self.head
#Iterate the Linked list
while(temp.next is not None):
temp=temp.next
#Insert the node at the end of the linked list
temp.next=Node(data)
#Function to get the middle element of the linked list
def Middleelement(self,head):
#Checking the base condition
if(head is None):
#Returning the head
return head
else:
#Creating two reference
#Slow Reference
slow=head
#Fast Reference
fast=head
while(fast.next !=None and fast.next.next!=None):
#Update the Fast Reference by two steps
fast=fast.next.next
#Update the slow Reference by one step
slow=slow.next
#Return the slow Reference
return slow
#Function to Perform the merge sort
def MergeSort(self,head):
#Checking the base condition
if(head ==None or head.next == None):
return head
else:
#Storing the middle of the Linked list
First=self.Middleelement(head)
#Creating Second part of the linked list
second=First.next
#Break the point of the first half to the second half
First.next=None
#Perform MergeSort on the First half
left=self.MergeSort(self.head)
#Perform MergeSort on the Second half
right=self.MergeSort(second)
#Call function to sort the both halves
SortedList=self.sort(First,second)
return SortedList
#Function to sort the two halves of the linked list
def sort(self,first,second):
#Checking the base conditions
if(first is None):
return second
if(second is None):
return first
#Creating Result reference
Result=None
#Checking the first node data of first part
if(first.data<=second.data):
Result=first
#Recursively call sort() Method again
Result.next=self.sort(first.next,second)
else:
Result=second
#Recursively call sort() Method again for next element
Result.next=self.sort(first,second.next)
#Return the sorted linked list
return Result
#Function to print the linked list
def print(self,head):
#Creating reference of the linked list
temp=head
list_=[]
#Iterate the linked list
while(temp is not None):
#Append the items of the linked list into the list_
list_.append(temp.data)
temp=temp.next
#Print the list
print(list_)
#Creating List reference of the Linked List
List=LinkedList()
#Inserting node in the Single list
List.push(11)
List.push(2)
List.push(1)
#Printing the original linked list
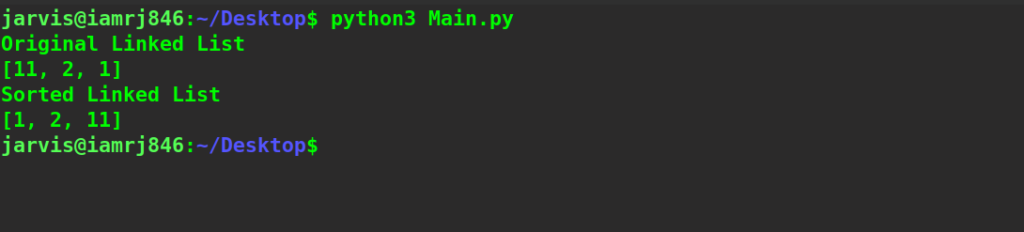
print("Original Linked List")
List.print(List.head)
#Printing the Reversed Linked List
print("Sorted Linked List")
List.Head=List.MergeSort(List.head)
List.print(List.Head)
Output:
C++
//Importing all the required libraries
#include
#include
#include<bits/stdc++.h>
using namespace std;
//Creating structure for the node of linked list
struct Node{
int data;//data to be stored to the node in the linked list
Node*next;//next reference to the node in the linked list
//Creating Constructor
Node(int data){
this->data=data; //Storing the data to the node
this->next=nullptr;
}
};
//Function to Transverse the Linked list
void print(Node *head){
//Checking if the Linked list is null or not
Node *temp=head;
if(temp==NULL){
return;
}
//Transverse the Linked List
while(temp!=NULL){
cout<data<<" "; temp=temp->next;
}
}
//Function to get the middle element of the given linked list
Node* Middleelement(Node *head){
//Checking the base condition
if(head==NULL){
//Return the head if the head is null
return head;
}
//Creating two reference for the linked list
//Slow Reference
Node *slow=head;
//Fast Reference
Node *fast=head;
//Iterate the Linked list using fast reference of the linked list
while(fast->next!=NULL && fast->next->next!=NULL){
//Update the slow pointer
slow=slow->next;
//Update the fast pointer
fast=fast->next->next;
}
//Return the slow reference that contains the middle element of the linked list
return slow;
}
//Function to sort the two halves of the linked list
Node* sortedMerge(Node *left,Node *right){
//Checking the base conditions
if(left==NULL){
return right;
}
if(right==NULL){
return left;
}
//Creating a temporary reference to refer the sorted linked list
Node *result=NULL;
//Checking if the left reference data is smaller than the right reference data
if(left->data<=right->data){
//Update the result reference
result=left;
//Recursively call the left.next for next node
result->next=sortedMerge(left->next, right);
}
else{
//Update the result reference
result=right;
//Recursively call the left.next for next node
result->next=sortedMerge(left, right->next);
}
//Return the sorted linked list
return result;
}
//Function to perform the merge sort of the linked list
static Node *mergeSort(Node* head){
//Checking the base conditions
if(head==NULL||head->next==NULL){
return head;
}
//Getting the middle element
Node *firsthalf=Middleelement(head);
//Creating second half of the linked list
Node *secondHalf=firsthalf->next;
//Break the middle element reference
firsthalf->next=NULL;
//Recursively call the two halves of the linked list
Node *left=mergeSort(head);
Node *right=mergeSort(secondHalf);
//call for the sorting
Node *sortedList=sortedMerge(left,right);
//Return the complete sorting linked list
return sortedList;
}
int main(){
//Creating Head of the linked list
Node *head =new Node(11);
//Creating Second node of the linked list
head->next=new Node(10);
//Creating third node of the linked list
head->next->next=new Node(9);
//Creating third node of the linked list
head->next->next->next=new Node(9);
//Printing Original Linked List
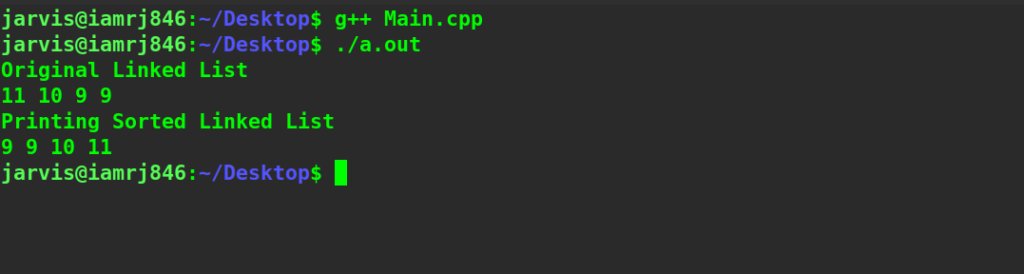
printf("Original Linked List\n");
print(head);
head=mergeSort(head);
printf("\n");
//Printing Sorted Linked List
printf("Printing Sorted Linked List");
printf("\n");
print(head);
return 0;
}
Output:
Complexity
- Time Complexity : The Time complexity of this approach is O(nlog(n).
- Space Complexity : The Space Complexity of this approach is O(1).
Conclusion
Merge Sort for Linked Lists is one of the most interesting problems of Data structure. In this article, we have discussed an approach to sort a linked list using Merge Sort. Sorting of linked lists is a little bit difficult due to the non-contiguous memory location of the nodes available in the linked list. But with little variation of the naive merge sort algorithm, we can easily sort the linked list desired order.
We hope this article will help you to understand the problem statement and you will be able to solve any other variation of this problem.
Happy Coding!
People are also reading:
- Rearrange an array in maximum minimum form
- Print a given matrix in spiral form
- Sort binary array in linear time
- What is Structured Programming?
- Construct a tree from Inorder and Level order traversals
- Write a Program to convert given inches into equivalent yard, and feet
- DSA Binary Search Tree
- Find minimum jumps required to reach the destination
- DSA: Binary Heap Tree
- Fibonacci Series





Leave a Comment on this Post