Principal component analysis (PCA) is a type of unsupervised algorithm that we use for dimensionality reduction. The concept is simple; remove the features that are similar or do not add any extra value in the decision-making so that the number of distinct features is less. Doing so reduces the processing time without compromising accuracy. Other popular dimensionality reduction algorithms are matrix factorization and linear discriminant analysis. In layman’s words, principal component analysis summaries the data by highlighting the important features while eliminating the less useful or less valuable features. PCA is widely used for exploratory data analysis (EDA) and predictive modeling. Invented by Karl Pearson in 1901 as the Principal axis theorem, it was later evolved and named PCA (Principal Component Analysis) in the 1930s by Harold Hotelling.
What is Principal Component Analysis?
Principal component analysis is a linear dimensionality reduction technique that converts a set of potentially correlated variables (features) into a set of linearly uncorrelated variables called principal components using orthogonal transformation. All the features are converted to numerical values before performing the transformation. A simple diagram to illustrate this is:
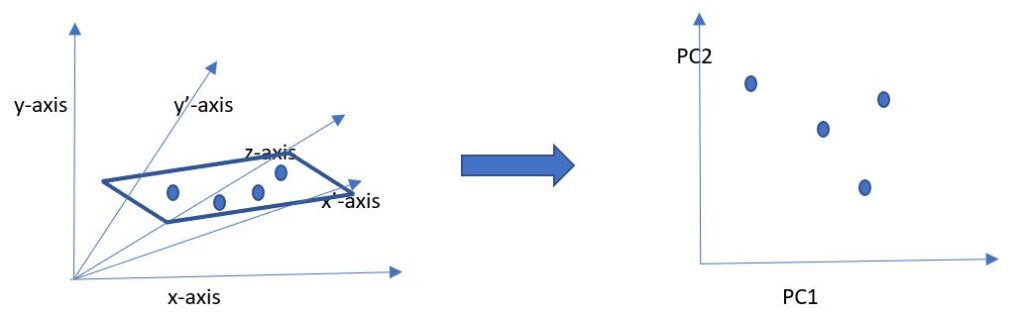
Diagram I
As we see, there are many variables in the original dataset, each representing an axis – x, y, z, x’, y’. After applying the algorithm, the variables are converted into a reduced set of principal components, PC1 and PC2.
So, What is Orthogonal Transformation?
Two or more variables are orthogonal if there is no correlation between the variables i.e. the value of correlation is zero. For example, if there is a vector v, and we want to transform it into another vector u by performing dot product (scalar multiplication) with a matrix then: u = Av, where A is the matrix If we transpose the matrix A, i.e. AT, and still get the same product, then the matrix is said to be orthogonal i.e.: u = ATv = Av This means we get the same dot product, even after
transposing the matrix
. Therefore, if we have an object that we represent as a vector, and if we just rotate (transpose) the matrix A (orthogonal transformation), we will still be able to retain all the properties of the vector. The object, thus, will be just flipped or rotated. For the sake of simplicity, let us take an example dataset with two dimensions. We will see the correlation between the X and Y variables, and then see how we can flip and rotate the linear plot (orthogonal transformation) to make it one-dimensional:
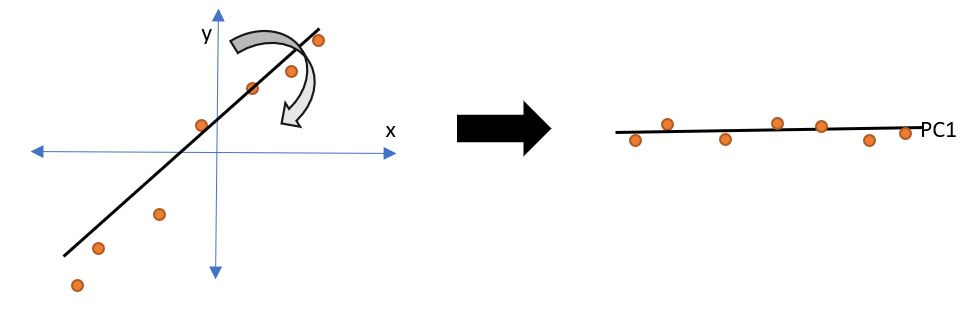
Diagram II
We can see that the coordinates x and y are plotted, and there is a positive correlation between the two variables. When we rotate the line that crosses maximum data points, we get a straight line, i.e. a single dimension, thus, we achieve dimensionality reduction.
Important Terms
Before digging deeper into the details of principal component analysis, let us understand the important concepts that we must know to perform the dimensionality reduction algorithm:
-
Dimensionality
This defines the number of features in the dataset. If your dataset has 100 columns, then the dimensionality will be 100.
-
Variance
Variance or covariance determines the difference between the actual and expected value of a random variable or feature. Mathematically, we define it as the average of squares of the difference between the actual and the expected values of a variable. Since we find the squares, the variance is always a positive value. In simple words, the variance is simply the measure of the change in something (from its expected value).
-
Eigenvector and Eigenvalue
Let us consider a non-zero vector v. If a square matrix (n x n), say A, when multiplied (scalar) with the vector v (i.e. Av), is a multiple of v, then the vector v is said to be the eigenvector of the square matrix A. It can be represented in the following equation: Av = ?v Here, v is the eigenvector and ? is the corresponding eigenvalue. As we know that a vector has both the direction and the value, applying linear transformation will not change the direction of the vector. Further, the eigenvector should be a non-null value. For easy reference, here is the equation again: (Square matrix A * EigenVector) – (EigenValue*EigenVector) = 0 Eigenvectors and eigenvalues help us understand and interpret data better. As such, we use them to transform data and represent the same in a more manageable form. Both concepts are vital for performing data science. As we will see later, it is elementary to calculate eigenvectors and eigenvalues using the NumPy library.
-
Correlation
Correlation is the extent or degree to which variables relate to each other. A positive correlation between A and B means that A increases with B and vice-versa. Similarly, a negative correlation between the two means that A increases when B decreases, and vice-versa. If there is no correlation between A and B, the value is 0. The value of correlation always lies between -1 and +1.
-
Principal Components
Principal component analysis reduces the n-dimensional space into a lesser dimension by reducing the number of variables. This reduction happens by choosing features that do not correlate with each other, i.e. they are orthogonal (or perpendicular) to each other. Such vectors minimize the averaged squared perpendicular distance from a point to the line. Repeating this process to minimize the distance forms an orthogonal basis wherein the individual data dimensions are uncorrelated (orthogonal). These basis vectors are Principal Components. PC1 and PC2 are principal components in diagram I above.
-
Feature Vector
As we know a vector has direction and value, we can, thus, represent it spatially. A feature vector is a vector that contains multiple elements (attributes) about an object. It represents an object’s numerical representation. For example, a feature can be a keyword, image, sound length, etc. For an image, a feature vector can contain information like color, size, shape, edges, intensity, and so on. We represent a feature vector as a matrix F: F = f1 f2 . . fn We get feature space by putting all the features together in a feature vector:
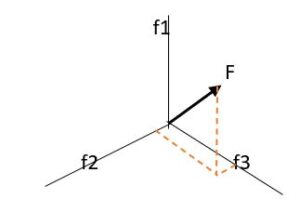
Diagram III
As we can represent feature vectors in many ways, they are an excellent choice for machine learning algorithms for data analysis.
How does the PCA Algorithm Work?
We already know that all the principal components resulting from the reduction are orthogonal. The principal components are nothing but the linear combinations of the original variables and follow the principle of least squares. We name PCs as per their importance, for example, PC1 should be the most important PC. PC2 should be less important than PC1. Likewise, important of PC3 < importance of PC2 and so on. This is because the variations in the components decrease when we move from PC1 (first) to PCn (last). So, how does this orthogonal transformation happen? How can we flip or rotate the dimensions and reduce them? The simple answer is by finding the components with the largest variance. Let us perform PCA step-by-step:
Step 1 - Standardization of variables
Initially, all the variables will have a different range of values. For example, the variable height of a human may range from 60 inches to 180 inches (or even more), whereas weight values may range from 10 kilograms to 100 kilograms. To find the correlation between both, we need to bring them to a comparable scale. If not, then the variables that have a larger range will overshadow the variables with smaller ranges. Thus, we would get biased results. Standardization is done using the following formula: s = (value – mean)/standard deviation Refer to our article on Statistics and probability to know how to calculate the above values.
Step 2 - Computing the covariance matrix
A covariance matrix helps determine the correlations between different variables in various possible pairs. If there is negative covariance, then the variables are indirectly proportional. If there is positive covariance, then the variables are directly proportional to each other. We represent the covariance matrix can as: C = Cov(a,a) Cov(a,b) Cov(b,a) Cov(b,b) Here, a and b are the variables and the matrix is a 2x2 or 2-dimensional matrix, meaning that there are 2 variables. If there are 10 dimensions, the covariance matrix will be a 10x10 matrix. Covariance matrix is commutative i.e. Cov(a,b) = Cov(b,a) Finding covariance helps us identify heavily dependent variables that contain biased and redundant information that can result in reduced model performance.
Step 3 - Calculating the eigenvector and eigenvalue
Eigenvector and eigenvalue are calculated from the covariance value. Remember that every eigenvector has an associated scalar value, called an eigenvalue. The sum of all the eigenvalues from the covariance matrix represents the total variance. The principal components are highly significant with the first component (PC1) being the most significant one. So, if there are 10 original variables in your dataset, then there will be 10 corresponding eigenvalues. Hence, 10 PCs. But the most important information will be in the first few PCs, and thus, we can eliminate the remaining PCs, somewhere from PC6 to PC10. Mathematically, Principal Components are the linear combinations of the initial variables and represent the direction of maximum variance . If you plot a graph, the PC will be a new axis containing the best angle to view the data. So, how do we identify which PC is most significant? It's simple. The one with the highest value of eigenvalue is the most significant PC.
Step 4 - Determine the principal components
We determine the principal components (PC) using the values of eigenvector and eigenvalue. We identify the components in such a way that they still preserve the important information in the data. If we arrange the eigenvectors in order from highest to lowest eigenvalue, we will get PC1 to PCn for an n-dimensional array. Suppose there are 3 variables in the dataset. The covariance matrix, therefore, will calculate 3 eigenvalues. Let’s say the values are 0.23 (?1), 1.34 (?2), 0.007(?3), respectively. We observe that, ?2 > ?1 > ?3 This means the eigenvector (v2) corresponding to the eigenvalue ?2 is PC1, v1 corresponding to ?1 is PC2, and v3 corresponding to ?3 is PC3.
Step 5 - Dimensionality reduction using principal component analysis
Once we know the principal components, we can reduce the dimensions of the data by applying the PCA algorithm. Thus, we get the reduced set of variables that we can process further for data analysis. Imagine having 1,000 variables in the original dataset and then reducing them into about 200 variables and then analyzing only those 200 variables with all the important information still intact. Obviously, it will save a lot of resources and time.
Pros and Cons of Principal Component Analysis
Just like everything else in the Universe, principal component analysis has its advantages and disadvantages. Most important among them are:
Advantages
- Removes all the correlated features from the dataset.
- With fewer features, the performance of the algorithm improves significantly.
- Since the variables (features are fewer), the problem of overfitting doesn’t occur.
- Makes the visualization of data easier because of lower dimensions.
Disadvantages
- It is essential to standardize the data and scale the features to find the correct principal components, which need conversion of all the features into numerical features.
- Since principal components are a linear combination of original features, they are not easily readable or interpretable.
- Information loss can happen if the principal components are not selected properly.
Implementing PCA in Python
It is very easy to implement PCA in Python, because of the friendly libraries it has. For this article, we will use the scikit-learn library, which implements PCA using decomposition. If you want a quick recap of Python , read our article on Python for data science. Let’s start with loading the dependencies (libraries):
import pandas as pd import numpy as np import StandardScaler from sklearn.preprocessing import matplotlib import matplotlib.pyplot as plt from sklearn.decomposition import PCA # load the data from your dataset using the pandas library <datasetname> = pd.read_csv(‘path to csv’) df1 = pd.Dataframe(<dataset>, columns = [required columns]) # Perform data processing on the original dataset like standardization, removing/replacing null values, converting variables into numerical values etc. X_std = StandardScaler().flt_transform(df1) #standardization # Find the covariance matrix mean_vectr = np.mean(X_std, axis=0) cov_matrix = (X_std – mean_vectr).T.dot(X_std – mean_vectr)/(X_std.shape[0]-1) # Calculate eigenvalue and eigenvector (eigendecomposition) cov_matrix = np.cov(X_std.T) eigen_values, eigen_vectors = np.linalg.eig(cov_matrix) # Sort the eigenvalues in descending order to find the principal components eigen_sorted = [(np.abs(eigen_values[i]), eigen_vectors[:,i]) for i in range(len(eigen_values)] # Apply PCA technique for dimensionality reduction pca = PCA(n_components = 2) pca.fit_transform(df1) pca = PCA().fit(X_std) # Plot the variance explained by each principal component plt.plot(np.cumsum(pca.explained_variance_ratio_)) plt.xlabel(‘Final number of features) plt.ylabel(‘Total explained variance’) plt.show()
Applications of Principal Component Analysis
There are several applications of the Principal Component Analysis dimensionality reduction technique in the fields of computer vision, facial recognition, and image compression. PCA is also used extensively in medical diagnosis, anomaly detection, bioinformatics, data mining, financial risk management, and spike sorting (neuroscience).
Conclusion
Finally, we are all caught up with PCA. Through this article, we tried to include as many details as possible about principal component analysis. It is reasonably straightforward when done judiciously. You need to practice understanding and find the principal components in your dataset. Since many ML libraries help you in the process, it is crucial to know how to use these libraries and frameworks. You should also be familiar with statistics and mathematics to understand the calculations for variance, mean square and other important parameters. People are also reading:





Leave a Comment on this Post