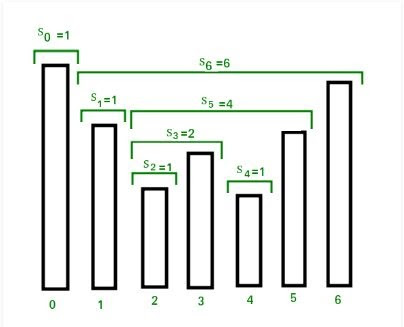
The Stock Span Problem is one of the famous financial problems where we have a list of prices of stocks of consecutive n days and we have to calculate the span of stock’s price for all the n days. The span of a particular day is defined as a maximum number of consecutive days before the day, for which the price of the stock on a particular day is less than or equal to the current day.
For Example :
Consider an array containing the price of sock for the 7 consecutive days .{200,60,140,120,150,170}, the span of these stocks for particular days will be {1,1,1,2,1,4, 6 }.
Input: {100,80,60,70,60,75}
Output: {1,1,1,2,1,4 }
Approach: (Naive Approach)
- This is a simple approach to solve this problem where we use two nested loops and check the price of all consecutive days before the current days.
- Calculate the consecutive number of days on which the price of the stack is smaller or equal to the current day’s stock price.
- Store the count of the number of days in an array or list.
- Return the array/List.
Java Programming
//Importing libraries
import java.util.*;
import java.io.*;
//Main class
class Main1{
//Function to print the span details of the stock
static void print(int span[]){
for(int details_:span){
System.out.print(details_+" ");
}
}
//Function to calculate the stock span
static int [] calulate_stockspan(int price_stock[],int length){
//Checking the base condition
if(length==0){
return null ;
}
//Creating an array to store the details of the stock
int span[]=new int[length];
//Minimum span will be 1
Arrays.fill(span, 1);
for(int i=0;i<price_stock.length;++i){ int count=1; for(int j=i-1;j>=0;--j){
//Checking the condition of the stock
if(price_stock[j]<=price_stock[i]){
//Increment the value
++count;
}
else{
break;
}
}
//Store the details of the span
span[i]=count;
}
//Return the span details
return span;
}
public static void main(String args[]){
//Array containing stock price
int price_stock[]={100,80,60,70,60,75};
//Length of the array
int length=price_stock.length;
//Function to calculate the span
int span[]=calulate_stockspan(price_stock, length);
//Print the span details
System.out.println("Stock_Span");
print(span);
}
}
Output:

Python Programming
#Function to calculate the span details
def calulate_stockspan(price_stock,length):
#Checking the base condition
if(length==0):
return 0
else:
span=[]
for i in range(len(price_stock)):
count=1
j=i-1
while j>=0:
#Checking the condition of the stock
if(price_stock[j]<=price_stock[i]):
#Increment the value
count=count+1
else:
break
j=j-1
#Insert the count
span.insert(i,count)
#Return the span details
return span
def main():
#List containing stock price
price_stock=[100,80,60,70,60,75]
#Length of the list
length=len(price_stock)
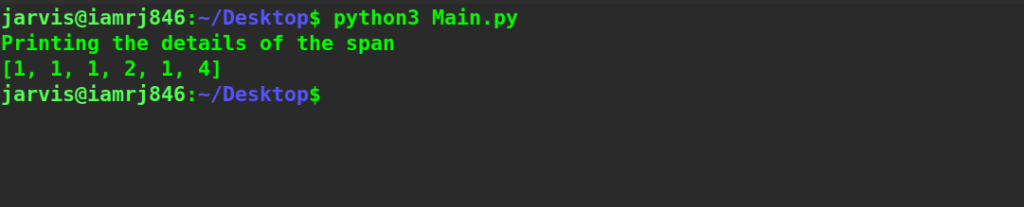
print("Printing the details of the span")
span=calulate_stockspan(price_stock, length)
print(span)
main()
Output:
C++ Programming
//Importing the libraries
# include<iostream>
# include <conio.h>
#include <bits/stdc++.h>
using namespace std;
//Function to calculate the span of the stock price on a particular day
void calulate_stockspan(int price_stock[],int length,int span[]){
//Checking the base condition
if(length==0){
return ;
}
for(int i=0;i<length;++i){ int count_=1; for(int j=i-1;j>=0;--j){
//Checking the condition of the stock
if(price_stock[j]<=price_stock[i]){
//Increment the value
++count_;
}
else{
break;
}
}
//Store the details of the span
span[i]=count_;
}
//Return the span details
}
void print(int span[],int length){
for(int i=0;i<length;++i){
cout<<span[i]<<" ";
}
}
int main(){
//Array containing stock price
int price_stock[]={100,80,60,70,60,75};
//Length of the array
int length=sizeof(price_stock)/sizeof(price_stock[0]);
//Creating an array to store the details of the stock
int span[length];
//Function to calculate the span
calulate_stockspan(price_stock, length,span);
//Print the span details
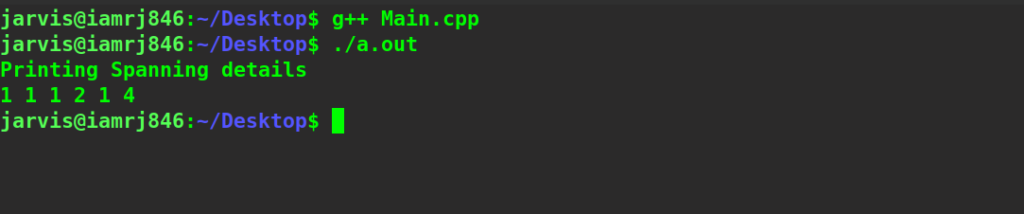
printf("%s\n","Printing Spanning details");
print(span,length);
return 0;
}
Output:
Complexity :
- Time Complexity : The Time complexity of this approach is O(n^n).
- Space Complexity : The Space Complexity of this approach is O(n).
Approach 2: (Optimised Approach)
- In this approach, we will use the stack data structure because of the LIFO property, which is the “Last in First out” of the stack data structure .
- Pop all indexes from the stack until the current index stock price becomes smaller than the upcoming index value from the stack.
- Check two conditions, if the stack is empty, the answer will be current index value+1.
- Otherwise, the answer will be the current index-peak element of the stack(span of stock).
- Push the current index into the stack.
C++ Programming
//Importing the libraries
# include <conio.h>
# include <iostream>
#include <bits/stdc++.h>
using namespace std;
//Function to calculate the span of the stock price
void calulate_stockspan(int price[],int length){
//Creating stack to store the index of the stock price
stackst;
//Creating Vector to store the span of particular price
vectorvc;
for(int i=0;i<length;++i){
//Checking the condition
while(!st.empty()&&(price[st.top()]<=price[i])){
//pop the element
st.pop();
}
//Checking if stack is empty or not
if(st.empty()){
//push the index into the vector
vc.push_back(i+1);
//Push the index of the current element into the stack
st.push(i);
}
else{
vc.push_back(i-st.top());
//Push the index of the current element into the stack
st.push(i);
}
}
//Print the span details
printf("%s\n","Printing Span details");
for(int i=0;i<length;++i){
//Printing the span details of the stock price
cout<<vc[i]<<" ";
}
}
int main(){
//Array containing stock price
int price_stock[]={100,80,60,70,60,75};
//Length of the array
int length=sizeof(price_stock)/sizeof(price_stock[0]);
//Function to calculate the span
calulate_stockspan(price_stock, length);
return 0;
}
Output:

Java Programming
//Importing the libraries
import java.util.*;
//Creating class
class Main1{
//Function to print the span details of the stock
static void print(int arr[]){
for(int i=0;i<arr.length;++i){
//Printing the span details
System.out.print(arr[i]+" ");
}
}
//Function to calculate the span details of the stock price
static int [] span(int arr[],int length){
//Creating stack to store the minimum stock price
StackS=new Stack();
//Creating array to store the span details
int span[]=new int[length];
for(int i=0;i<length;++i){
//Checking the condition
while(!S.empty()&& arr[S.peek()]<=arr[i]){
//Pop the index from the array
S.pop();
}
//Checking the condition
if(S.empty()){
//Push the element into the stack
S.add(i);
//Update the array
span[i]=i+1;
}
else{
span[i]=i-S.peek();
S.add(i);
}
}
//Return the span array
return span;
}
public static void main(String args[]){
int arr[]={100,80,60,70,60,75,85};
int length=arr.length;
//Call function to calculate the span details of the stock price and returning the array
int span[]=span(arr,length);
System.out.println("Printing the Span Details");
print(span);
}
}
Output:

Python Programming
#Function to calculate the span details
def calulate_stockspan(price_stock,length):
#Checking the base condition
if(length==0):
return 0
else:
st=[]
#List for storting the span details
span=[]
for i in range(len(price_stock)):
#Pop the elements from the stack until the condition is true
while(len(st)>0 and price_stock[st[-1]]<=price_stock[i]):
st.pop()
#Checking the base condition
if(len(st)==0):
#Append the new element details
span.append(i+1)
st.append(i)
else:
span.append(i-st[-1])
st.append(i)
#Return the span details
return span
def main():
#List containing stock price
price_stock=[100,80,60,70,60,75]
#Length of the list
length=len(price_stock)
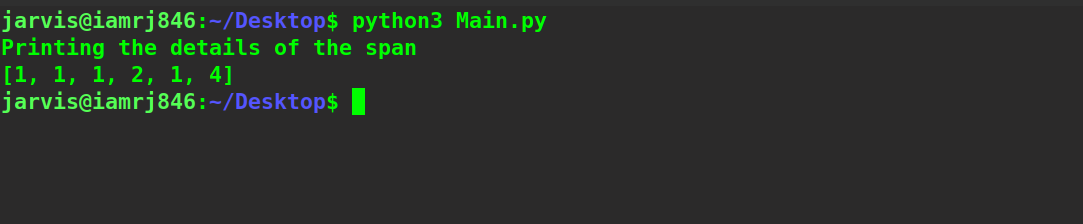
print("Printing the details of the span")
span=calulate_stockspan(price_stock, length)
print(span)
main()
Output:
Complexity :
- Time Complexity : The Time complexity of this approach is O(n).
- Space Complexity : The Space Complexity of this approach is O(n).
Approach 3: (Recursive Approach)
- In this approach, we use simple recursion to calculate the stock span of every stock price of a particular day.
- Iterate a loop and call a recursive function to all previous indexes and count the total number of days for which the price of the current element is larger or equal to all previous consecutive days.
- Store the count in an array.
- Return the array. The array will contain all the span details of all the stock prices.
Java Programming
//Importing libraries
import java.util.*;
import java.io.*;
//Main class
class Main1{
//Function to print the span details of the stock
static void print(int span[]){
for(int details_:span){
//Printing the stock span
System.out.print(details_+" ");
}
}
static int span_recursive(int previous_index,int starting_index,int price_stock[],int price){
//Checking base condition
if(previous_index<0){ return 0; } //Checking the price of previous day stock if(price_stock[previous_index]>price){
return 1;
}
//Call next previous day stock
int span=1+ span_recursive(previous_index-1, starting_index, price_stock, price);
//Return the answer
return span;
}
//Function to calculate the stock span
static void calulate_stockspan(int price_stock[],int length,int starting_index,int span[]){
for(int i=starting_index;i<length;++i){
//Call recursive function to calculate individual stock span
int ans=span_recursive(i-1,i,price_stock,price_stock[i]);
span[i]=ans;
}
}
public static void main(String args[]){
//Array containing stock price
int price_stock[]={100,80,60,70,60,75};
//Length of the array
int length=price_stock.length;
int span[]=new int[length];
//Function to calculate the span
calulate_stockspan(price_stock, length,1,span);
//Print the span details
System.out.println("Printing stock span details");
span[0]=1;
print(span);
}
}
Output:

C++ Programming
//Importing the libraries
# include <iostream>
#include <bits/stdc++.h>
using namespace std;
int span_recursive(int previous_index,int starting_index,int price_stock[],int price){
//Checking base condition
if(previous_index<0){ return 0; } //Checking the price of previous day stock if(price_stock[previous_index]>price){
return 1;
}
//Call next previous day stock
int span=1+ span_recursive(previous_index-1, starting_index, price_stock, price);
//Return the answer
return span;
}
//Function to calculate the span of the stock price on a particular day
void calulate_stockspan(int price_stock[],int length,int starting_index,int span[]){
for(int i=starting_index;i<length;++i){
//Call recursive function to calculate individual stock span
int ans=span_recursive(i-1,i,price_stock,price_stock[i]);
span[i]=ans;
}
}
void print(int span[],int length){
for(int i=0;i<length;++i){
cout<<span[i]<<" ";
}
}
int main(){
//Array containing stock price
int price_stock[]={100,80,60,70,60,75};
//Length of the array
int length=sizeof(price_stock)/sizeof(price_stock[0]);
//Creating an array to store the details of the stock
int span[length];
//Function to calculate the span
calulate_stockspan(price_stock, length,1,span);
//Print the span details
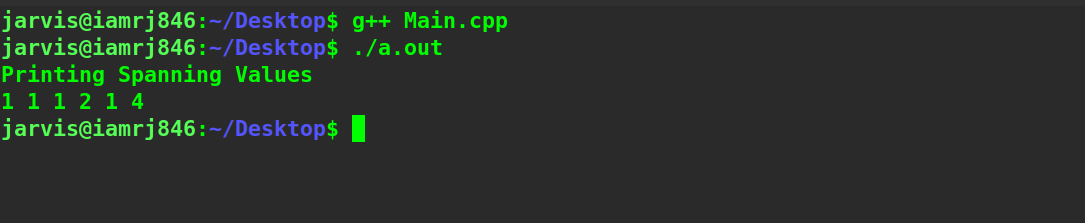
printf("%s\n","Printing Spanning Values");
span[0]=1;
print(span,length);
return 0;
}
Output:
Python Programing
#Function to calculate the span details
def span_recursive(previous_index, starting_index, price_stock, price):
#Checking the base condition
if(previous_index<0): return 0 if(price_stock[previous_index]>price):
return 1
#Call to the previous day for the span
return 1+span_recursive(previous_index-1,starting_index,price_stock,price)
#Function to calculate the span of the stock
def calulate_stockspan(price_stock, starting_index,length, span):
i=starting_index
while(i<length):
#Recursively call previous day
ans=span_recursive(i-1,i,price_stock,price_stock[i])
span.append(ans)
i=i+1
def main():
#List containing stock price
price_stock=[100,80,60,70,60,75]
#Length of the list
span=[]
length=len(price_stock)
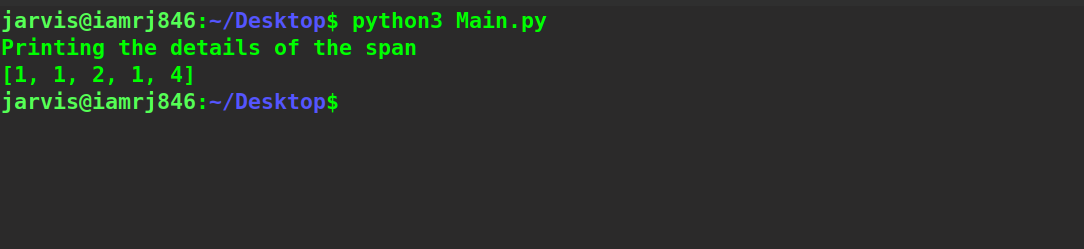
print("Printing the details of the span")
calulate_stockspan(price_stock, 1,length,span)
print(span)
main()
Output :
 Complexity
:
Complexity
:
- Time Complexity : The Time complexity of this approach is O(n^n).
- Space Complexity : The Space Complexity of this approach is O(n).
Conclusion
The Stock Span Problem is one of the most interesting problems of Data structure. In this article, we have discussed three approaches to solve The Stock Span Problem. One is the naive approach, the next one is the recursive implementation of the naive approach, and the third one is the optimized approach of this problem using the stack data structure. There are so many variations that can be made from this problem and this problem is most commonly asked during technical interviews. We hope this article will help you to understand the problem statement and you will be able to solve any other variation of this problem. Happy Coding! People are also reading:





Leave a Comment on this Post