Linear Programming - Definition, Types, and Applications

Optimization plays a vital role in every aspect of our lives. From managing problems at the workplace to working productively, we often look for optimization. This implies making the most out of the resources and time available to solve a specific problem.

In our everyday lives, we encounter several optimization problems where we try to maximize the result and minimize the required effort. To solve them, there are a lot of techniques. Among all, linear programming is the most popular one. In this article, we shall introduce you to linear programming.

So, let us get started without any further ado!

What is Linear Programming?

Linear programming is a mathematical approach to finding the optimal solution to a given problem. An optimal solution refers to the best possible solution from the given set of parameters or requirements having linear relationships.

Simply put, it is a method of determining how to do a particular task with the minimum utilization of resources and attain the best possible results.

It is the combination of two different words: linear and programming. Linear implies the relationship between multiple variables with degree one, while programming refers to selecting the best possible solution out of multiple options available.

So, linear programming (LP) is a technique of selecting the best possible outcome among the available ones for a given solution that requires minimum resource utilization. It also refers to considering different inequalities associated with a situation and evaluating the best value to be obtained.

Maximizing the profit or minimizing the cost is the main goal while trying to solve a linear programming problem (LPP) as efficiently as possible. Due to this reason, it is also referred to as linear optimization.

Leonid Kantorovich, in 1937, during World War II, first introduced the concept of LP or linear optimization. It was used to determine expenditures and returns in such a way that it resulted in reduced military costs.

Computer modeling or simulation widely leverages the LP technique to come up with the best solution while allocating finite resources, including money, energy, manpower, time, space, and machine resources. Besides mathematics, this technique is also utilized in business, economics, telecommunications, and manufacturing.

Linear Programming to Solve Optimization Problems

Many of us might have experienced target-based situations in daily life. Let us take a few examples of target-based situations. Say a salesperson needs to achieve the specific target of selling products or services in a month. Or consider a student needs to finish the project within 20 days or an individual needs to buy an electronic gadget within a specific budget.

In the above examples, each individual aims to achieve their target with maximum benefits or minimize the cost. For instance, the students will aim to finish the given project within the given deadline and score maximum marks. The salesperson will work hard to achieve the sales target within a month. Meanwhile, the individual desiring to buy an electronic gadget will try to search for it at the minimum cost possible.

All the aforementioned problems are kinds of optimization problems. These problems aim to find out the maximum profit, minimum cost, or minimum use of resources. Optimization problems can be as simple as stated above as well as complicated.

There is one important aspect of optimization problems called the limiting factor. This factor implies the scarcity of resources. In our first example, the limiting factor is time, as the student needs to complete the project within 15 days.

Similarly, the limiting factor in the second example, i.e., salesperson, is time, as he/she needs to sell a certain amount of products within a month. Meanwhile, the limiting factor in the third example is the budget, as the individual needs to buy the gadget within a predetermined budget.

Example of a Linear Programming Problem

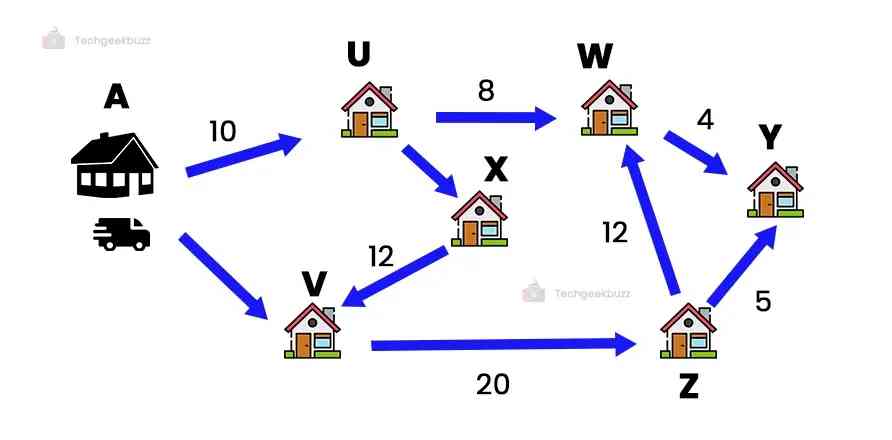
Let us consider a delivery boy with six different packages to be delivered today. As shown in the image above, the warehouse is situated at point A, and 6 different destinations where the delivery body needs to go are U, V, W, X, Y, and Z.

You can see the arrows between different locations and numbers on those arrows. These numbers represent the distance between two locations. In order to utilize the minimum resources (fuel and time), the delivery boy takes the shortest route between the locations.

As a result, the delivery boy will first calculate the distance for all possible routes for going to 6 different locations and, finally, decide on the shortest one. The delivery boy needs to deliver packages on time at all locations. This is where linear programming comes into play.

This technique will help the delivery boy to choose the optimal solution within the given constraints. Here, the real-life problems are formulated into mathematical models.

But can the six lines or routes between different locations be straight in real life? Obviously, no, because the real-life routes are not straight and involve turns, U-turns, traffic, and many other elements. Just with a simple assumption, we have reduced the complexity of the problem.

Characteristics of Linear Programming

Here are some common terminologies related to linear programming that one must know before solving linear programming problems (LPP).

• Decision Variables: These are the variables that decide the output. In other words, they are variables that compete with each other to share resources. They have a linear relationship and are interrelated. In addition, decision variables have the ability to decide the best and optimum solution for a given problem. To solve any problem, the first step is to identify decision variables.
• Objective Function: The given problem should have a clear objective that you can state quantitatively, such as maximizing profit or minimizing the cost. So, for a certain problem, you want to maximize profit, and it becomes your objective function.
• Constraints: Constraints are restrictions or limitations on the available resources or decision variables. The resources include the number of machines, labor materials, etc.
• Redundant Constraint: Redundant or non-negative constraints are restrictions that do not hinder the process of solving a problem.
• Feasible Solution: It is the collection of all possible solutions in the form of variables that meet the constraints.
• Optimum Solution: An optimum solution is the best solution among all solutions and complies with the objective of the problem in the best possible way.
• Linearity: This states that the relationship between two or more variables in a function must be linear, i.e., the degree of the variable should be one.

Components of Linear Programming

There are four components of LP, as follows:

• Decision Variables
• Constraints
• Data
• Objective Functions

Types of Linear Programming Problems (LPP)

A linear programming problem (LPP) is a problem that focuses on finding the optimal value of the given linear function. This optimal value can either be minimum or maximum, and the given linear function is assumed as the objective function.

This objective function comprises multiple variables that are subjected to certain conditions. Also, the objective function has to meet certain linear inequalities called linear constraints.

You can use LPP to get the optimal solution to a variety of problems, including manufacturing problems, diet problems, allocation problems, transportation problems, etc.

How to Formulate a Linear Programming Problem (LLP)?

The following are a few steps to formula any LP problem:

• First, identify decision variables that you need for formulating and later decide on the objective function.
• Next, define the objective function, i.e., define the business objectives in a mathematical form.
• List all constraints or limitations using decision variables in the mathematical form.
• Finally, identify and list all non-negative constraints.

Methods to Solve Linear Programming Problems (LLP)

There are different ways to solve LPP. These methods are as follows:

• Graphical Method

It is the most basic approach to solving LLP in two variables. When you have only two decision variables to consider, the graphical method comes in handy. It entails creating a set of linear inequalities and subjecting them to relevant conditions.

Further, it involves plotting equations on the X-Y plane, and the area of intersection that you get after plotting equations is the feasible area. This area provides the optimal solution and represents the model’s values.

• Simplex Method

This method employs an iterative approach to solving LLP and arriving at the best possible solution. Here, the value of the basic variable gets changed until the maximum or minimum value for the objective function is obtained.

• R

R is a programming language as well as a software environment for data analysis and data science . With R’s IpSolve package , it becomes easy to perform optimization with just a few lines of code.

• OpenSolve

It is an open-source linear optimizer tool for Excel that works for up to 100 variables. There are many other open-source optimization tools, such as MATLAB, Gurobi, CPLEX, etc.

Advantages of Linear Programming

Here are the worth-mentioning benefits of LP:

• LP can serve as a decision-making solution for businesses and help them find the optimal solution by keeping in mind the scarcity of available resources.
• It is a structured approach to solving real-world, target-based problems and helps businesses in making actionable decisions.
• It provides businesses with multiple solutions where decision-makers can analyze those solutions and choose the best and most profitable one.
• You can also leverage LP for changing situations. You can add extra constraints or change the existing ones to get the revised outcome.

Applications of Linear Programming

Some of the common applications of LP are as follows:

• In the production industry, LP helps teams decide on the production mix, production planning, and assembly line balancing.
• The oil industry leverages LP to determine the optimum quality of the oil by combining the appropriate proportions of different crude oils, octane, etc.
• In the sales and marketing domain, LP is widely used in plant location, media selection, and reducing the salesperson’s cost of traveling.
• Call centers and hospitals utilize LP for scheduling the shifts of employees.
• In the finance industry, LP helps businesses make decisions about spending money and from where to get the money such that the return is maximum.

Conclusion

Here ends our discussion on linear programming. Often referred to as linear optimization, LP is a mathematical technique for finding the optimal solution to a given problem. In simple terms, it helps you decide how to solve a problem by utilizing the resources minimally and still achieving the best possible results.

Many industry verticals employ LP to solve optimization challenges that they face frequently. However, the graphical method to solve LLP is not sufficient to solve more complicated business optimization problems. For this, you need to have a better grasp of tools and programming languages to solve optimization problems using linear programming.

People are also reading:

• What is Structured Programming?
• What is Pair Programming?
• Programming Paradigm
• R vs MATLAB
• R vs Python
• QuickSelect Algorithm
• Quicksort algorithm using Hoare’s partitioning scheme
• Quicksort using Dutch National Flag Algorithm
• Longest Consecutive Sequence in Linear time
• Sort binary array in linear time