Construct a Binary Tree from Inorder and Preorder traversals

You are given inorder and preorder traversals. Create a Binary Tree using these given traversals.

Inorder: In this traversal, we first visit the left subtree, then the root node, and the right subtree at the end.

Preorder: In this traversal, we first visit the root node, then the left subtree, and the right subtree at the end.

Example 1:

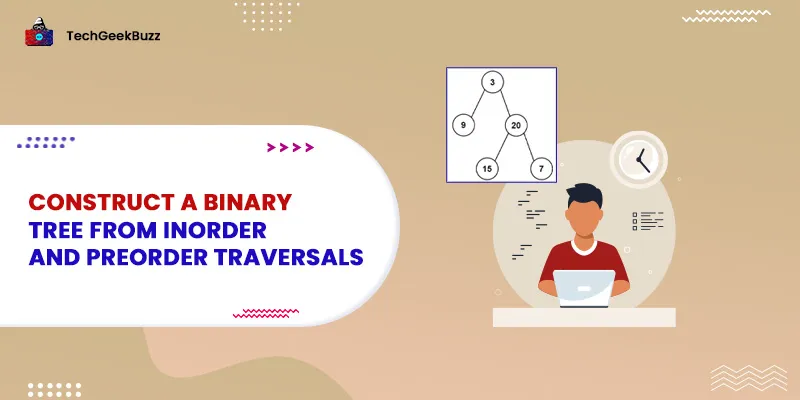
Input: 
preorder = [3,9,20,15,7], 
inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

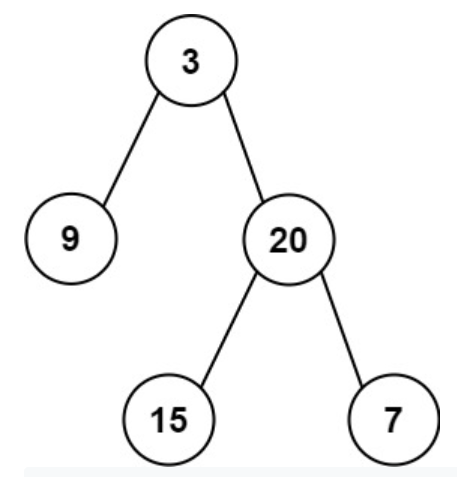
Explanation: As we already know that the first element of the preorder array is the root node. Therefore, 3 will be the root of the tree. Then, we can get the elements of the left subtree by simply searching 3 in the inorder array as the elements of the left subtree reside before the root node in the inorder array. Similarly, elements on the right side of 3 in the inorder array would be the elements of the right subtree. Hence, we get the output: [3,9,20,null,null,15,7]

Approach 1

The idea is that, as we know, the first element of the preorder array is the root node. Then, we can get the elements of the left subtree by simply searching the root element in the inorder array, as the elements of the left subtree reside before the root node in the inorder array. Similarly, elements on the right side of the root element in the inorder array would be the elements of the right subtree.

Algorithm

1. Take the first element of the preorder array, which will be the root node.
2. Create a new node as tNode and pass the element taken in the first step as the data.
3. Iterate over the inorder array to find the index of the picked element. Let the index be inIndex.
4. Make a function buildTree. The elements before the picked element will fall under the left subtree.
5. The elements after the picked element will fall under the right subtree.
6. Return tNode.

The implementation of the above-discussed approach is:

C++ Programming

#include<bits/stdc++.h>
using namespace std;

// Class for a node
// having an integer value, data
// and two pointers
// to store the references of the
// left and right children
class node
{
	public:
	char data;
	node* left;
	node* right;
};

// declaring prototypes of the methods to be used
int findIndex(char arr[], int strt, int end, char value);
node* newNode(char data);

// method to build a binary tree
// from the given 2 arrays of integers, 
// inorder & preorder. 
node* constructBinaryTree(char in[], char pre[], int inStrt, int inEnd)
{
	static int preIndex = 0;

	if (inStrt > inEnd)
		return NULL;

	// create a new node and 
	// assign it the value of the current node
	// using the preIndex.
	// Update the preIndex variable
	// so that it can be used for next recursive calls.
	node* tNode = newNode(pre[preIndex++]);

	// return if the new created node does not have children.
	if (inStrt == inEnd)
		return tNode;

	// otherwise, compute its height
	// in the inorder traversal.
	int inIndex = findIndex(in, inStrt, inEnd, tNode->data);

	// build left and right subtrees, with the help of 
	// inIndex in the inorder array.
	tNode->left = constructBinaryTree(in, pre, inStrt, inIndex - 1);
	tNode->right = constructBinaryTree(in, pre, inIndex + 1, inEnd);

	return tNode;
}

// defining the method findIndex,
// that searches the index of the given 
// value, passed as the parameter.
int findIndex(char arr[], int strt, int end, char value)
{
	int i;
	for (i = strt; i <= end; i++) { if (arr[i] == value) return i; } return i; } // method to create a node // with the value being set as the data // that is passed as the parameter, // and initializing its left and right children to NULL node* newNode(char data) { node* Node = new node(); Node->data = data;
	Node->left = NULL;
	Node->right = NULL;

	return (Node);
}

// method to print the 
// constructed tree.
void printTree(node* node)
{
	if (node == NULL)
		return;

	// recursively print the left subtree
	printTree(node->left);

	// print the root data
	cout<data<<" "; // recursively print the right subtree printTree(node->right);
}

/* Driver code */
int main()
{
	char in[] = { 'D', 'B', 'E', 'A', 'F', 'C' };
	char pre[] = { 'A', 'B', 'D', 'E', 'C', 'F' };
	int len = sizeof(in) / sizeof(in[0]);
	node* root = constructBinaryTree(in, pre, 0, len - 1);

	cout << "Constructed Tree is (Inorder Traversal): \n";
	printTree(root);
}

Output

Constructed Tree is (Inorder Traversal): 
D B E A F C

Java Programming

// Class for a node
// having an integer value, data
// and two pointers
// to store the references of the
// left and right children
class Node {
	char data;
	Node left, right;

	Node(char item)
	{
		data = item;
		left = right = null;
	}
}

class BinaryTree {
	Node root;
	static int preIndex = 0;

	// function to build a binary tree
	// from the given 2 arrays of integers, 
	// inorder & preorder.
	Node constructBinaryTree(char in[], char pre[], int inStrt, int inEnd)
	{
		if (inStrt > inEnd)
			return null;

		// create a new node and 
		// assign it the value of the current node
		// using the preIndex.
		// Update the preIndex variable
		// so that it can be used for next recursive calls
		Node tNode = new Node(pre[preIndex++]);

		// return if the new created node does not have children.
		if (inStrt == inEnd)
			return tNode;

		// otherwise, compute its height
		// in the inorder traversal.
		int inIndex = findIndex(in, inStrt, inEnd, tNode.data);

		// build left and right subtrees, with the help of 
		// inIndex in the inorder array.
		tNode.left = constructBinaryTree(in, pre, inStrt, inIndex - 1);
		tNode.right = constructBinaryTree(in, pre, inIndex + 1, inEnd);

		return tNode;
	}

	// defining the function findIndex,
	// that searches the index of the given 
	// value, passed as the parameter.
	int findIndex(char arr[], int strt, int end, char value)
	{
		int i;
		for (i = strt; i <= end; i++) {
			if (arr[i] == value)
				return i;
		}
		return i;
	}


	// function to print the 
	// constructed tree.
	void printTree(Node node)
	{
		if (node == null)
			return;

		// recursively print the left subtree
		printTree(node.left);

		// print the root data
		System.out.print(node.data + " ");

		// recursively print the right subtree
		printTree(node.right);
	}

	public static void main(String args[])
	{
		BinaryTree tree = new BinaryTree();
		char in[] = new char[] { 'D', 'B', 'E', 'A', 'F', 'C' };
		char pre[] = new char[] { 'A', 'B', 'D', 'E', 'C', 'F' };
		int len = in.length;
		Node root = tree.constructBinaryTree(in, pre, 0, len - 1);

		System.out.println("Constructed Tree is (Inorder Traversal): ");
		tree.printTree(root);
	}
}

Output

Constructed Tree is (Inorder Traversal): 
D B E A F C

Python Programming

# Class for a node
# having an integer value, data
# and two pointers
# to store the references of the
# left and right children
class Node:
	
	def __init__(self, data):
		self.data = data
		self.left = None
		self.right = None

# function to build a binary tree
# from the given 2 arrays of integers, 
# inorder & preorder.
def constructBinaryTree(inOrder, preOrder, inStrt, inEnd):
	
	if (inStrt > inEnd):
		return None

	# create a new node and 
	# assign it the value of the current node
	# using the preIndex.
	# Update the preIndex variable
	# so that it can be used for next recursive calls
	tNode = Node(preOrder[constructBinaryTree.preIndex])
	constructBinaryTree.preIndex += 1

	# return if the new created node does not have children.
	if inStrt == inEnd :
		return tNode

	# otherwise, compute its height
	# in the inorder traversal.
	inIndex = findIndex(inOrder, inStrt, inEnd, tNode.data)
	
	# build left and right subtrees, with the help of 
	# inIndex in the inorder array.
	tNode.left = constructBinaryTree(inOrder, preOrder, inStrt, inIndex-1)
	tNode.right = constructBinaryTree(inOrder, preOrder, inIndex + 1, inEnd)

	return tNode

# defining the function findIndex,
# that searches the index of the given 
# value, passed as the parameter.
def findIndex(arr, start, end, value):
	for i in range(start, end + 1):
		if arr[i] == value:
			return i
# function to print the 
# constructed tree.
def printTree(node):
	if node is None:
		return
	
	# recursively print the left subtree
	printTree(node.left)
	
	# print the root data
	print (node.data, end = " ")

	# recursively print the right subtree
	printTree(node.right)
	
# Driver program 
inOrder = ['D', 'B', 'E', 'A', 'F', 'C']
preOrder = ['A', 'B', 'D', 'E', 'C', 'F']

constructBinaryTree.preIndex = 0
root = constructBinaryTree(inOrder, preOrder, 0, len(inOrder)-1)


print ("Constructed Tree is (Inorder Traversal):")
printTree(root)

Output

Constructed Tree is (Inorder Traversal): 
D B E A F C

C# Programming

using System;

// Class for a node
// having an integer value, data
// and two pointers
// to store the references of the
// left and right children
public class Node {
	public char data;
	public Node left, right;

	public Node(char item)
	{
		data = item;
		left = right = null;
	}
}

public class Tree {
	public static Node root;
	public static int preIndex = 0;

	// function to build a binary tree
	// from the given 2 arrays of integers, 
	// inorder & preorder. 
	public virtual Node convertBinaryTree(char[] arr, char[] pre,
								int inStrt, int inEnd)
	{
		if (inStrt > inEnd) {
			return null;
		}

		// create a new node and 
		// assign it the value of the current node
		// using the preIndex.
		// Update the preIndex variable
		// so that it can be used for next recursive calls.
		Node tNode = new Node(pre[preIndex++]);

		// return if the new created node does not have children.
		if (inStrt == inEnd) {
			return tNode;
		}

		// otherwise, compute its height
		// in the inorder traversal.
		int inIndex = findIndex(arr, inStrt,
							inEnd, tNode.data);

		// build left and right subtrees, with the help of 
		// inIndex in the inorder array.
		tNode.left = convertBinaryTree(arr, pre, inStrt, inIndex - 1);
		tNode.right = convertBinaryTree(arr, pre, inIndex + 1, inEnd);

		return tNode;
	}

	// defining the function findIndex,
	// that searches the index of the given 
	// value, passed as the parameter.
	public virtual int findIndex(char[] arr, int strt,
							int end, char value)
	{
		int i;
		for (i = strt; i <= end; i++) {
			if (arr[i] == value) {
				return i;
			}
		}
		return i;
	}

	// function to print the 
	// constructed tree.
	public virtual void printTree(Node node)
	{
		if (node == null) {
			return;
		}

		// recursively print the left subtree
		printTree(node.left);

		// print the root data
		Console.Write(node.data + " ");

		// recursively print the right subtree
		printTree(node.right);
	}

	public static void Main(string[] args)
	{
		Tree tree = new Tree();
		char[] arr = new char[] { 'D', 'B', 'E', 'A', 'F', 'C' };
		char[] pre = new char[] { 'A', 'B', 'D', 'E', 'C', 'F' };
		int len = arr.Length;
		Node root = tree.convertBinaryTree(arr, pre, 0, len - 1);

		Console.WriteLine("Constructed Tree is (Inorder Traversal):");
		tree.printTree(root);
	}
}

Output

Constructed Tree is (Inorder Traversal): 
D B E A F C

Complexity Analysis

Time Complexity : O(n) where n is the number of nodes of the Binary Tree. We are simply linearly iterating the tree

Approach 2

This approach is more optimized than the previous one. We will be using hashing in this method to store the indices.

Algorithm

1. Create a node with the value being set as the data that is passed as the parameter and initializing its left and right children to NULL.
2. Create a new node and assign it the value of the current node using the preIndex.
3. Update the preIndex variable so that it can be used for the next recursive calls.
4. Return if the newly created node does not have children.
5. Otherwise, compute its height in the inorder traversal.
6. Build left and right subtrees with the help of inIndex in the inorder array.

The implementation of the above-discussed approach is:

C++ Programming

#include <bits/stdc++.h>
using namespace std;

// Structure for a node
// having an integer value, data
// and two pointers
// to store the references of the
// left and right children
struct Node {
	char data;
	struct Node* left;
	struct Node* right;
};

// function to create a node
// with the value being set as the data
// that is passed as the parameter,
// and initializing its left and right children to NULL
struct Node* newNode(char data)
{
	struct Node* node = new Node;
	node->data = data;
	node->left = node->right = NULL;
	return (node);
}

// function to build a binary tree
// from the given 2 arrays of integers, 
// inorder & preorder.
struct Node* convertBinaryTree(char in[], char pre[], int inStrt,
					int inEnd, unordered_map<char, int>& mp)
{
	static int preIndex = 0;

	if (inStrt > inEnd)
		return NULL;

	// create a new node and 
	// assign it the value of the current node
	// using the preIndex.
	// Update the preIndex variable
	// so that it can be used for next recursive calls.
	char curr = pre[preIndex++];
	struct Node* tNode = newNode(curr);

	// return if the new created node does not have children.
	if (inStrt == inEnd)
		return tNode;

	// otherwise, compute its height
	// in the inorder traversal.
	int inIndex = mp[curr];

	// build left and right subtrees, with the help of 
	// inIndex in the inorder array.
	tNode->left = convertBinaryTree(in, pre, inStrt, inIndex - 1, mp);
	tNode->right = convertBinaryTree(in, pre, inIndex + 1, inEnd, mp);

	return tNode;
}

// wrapper function for the convertBinaryTree function 
// that creates a map 
struct Node* convertBinaryTreeWrap(char in[], char pre[], int len)
{
	// hold the indices of all elements in
	// the unorderd map.
	unordered_map<char, int> mp;
	for (int i = 0; i < len; i++) mp[in[i]] = i; return convertBinaryTree(in, pre, 0, len - 1, mp); } // function to print the // constructed tree. void printTree(struct Node* node) { if (node == NULL) return; printTree(node->left);
	cout << node->data << " "; printTree(node->right);
}

int main()
{
	char in[] = { 'D', 'B', 'E', 'A', 'F', 'C' };
	char pre[] = { 'A', 'B', 'D', 'E', 'C', 'F' };
	int len = sizeof(in) / sizeof(in[0]);

	struct Node* root = convertBinaryTreeWrap(in, pre, len);

	cout << "Constructed Tree is (Inorder Traversal): \n";
	printTree(root);
}

Output

Constructed Tree is (Inorder Traversal): 
D B E A F C

Java Programming

import java.io.*;
import java.util.*;

// Class for a node
// having an integer value, data
// and two pointers
// to store the references of the
// left and right children
class Node
{
char data;
Node left,right;
Node(char item)
{
	data = item;
	left = right = null;
}
}
class Tree
{

public static Node root;

// hold the indices of all elements in
// the unorderd map.
static HashMap<Character,Integer> mp = new HashMap<>();
static int preIndex = 0;

// function to build a binary tree
// from the given 2 arrays of integers, 
// inorder & preorder.
public static Node convertBinaryTree(char[] in, char[] pre, int inStrt, int inEnd)
{

	if(inStrt > inEnd)
	{
	return null;
	}

	// create a new node and 
	// assign it the value of the current node
	// using the preIndex.
	// Update the preIndex variable
	// so that it can be used for next recursive calls.
	char curr = pre[preIndex++];
	Node tNode;
	tNode = new Node(curr);

	// return if the new created node does not have children.
	if (inStrt == inEnd)
	{
	return tNode;
	}

	// otherwise, compute its height
	// in the inorder traversal.
	int inIndex = mp.get(curr);

	// build left and right subtrees, with the help of 
	// inIndex in the inorder array.
	tNode.left = convertBinaryTree(in, pre, inStrt, inIndex - 1);
	tNode.right = convertBinaryTree(in, pre, inIndex + 1, inEnd);
	return tNode;
}

// wrapper function for the convertBinaryTree function 
// that creates a map 
public static Node convertBinaryTreeWrap(char[] in, char[] pre, int len)
{
	for(int i = 0; i < len; i++)
	{
	mp.put(in[i], i);
	}
	return convertBinaryTree(in, pre, 0, len - 1);
}

// function to print the 
// constructed tree.
static void printTree(Node node)
{
	if(node == null)
	{
	return;
	}
	printTree(node.left);
	System.out.print(node.data + " ");
	printTree(node.right);
}

public static void main (String[] args)
{
	char[] in = {'D', 'B', 'E', 'A', 'F', 'C'};
	char[] pre = {'A', 'B', 'D', 'E', 'C', 'F'};
	int len = in.length;

	Tree.root=convertBinaryTreeWrap(in, pre, len);

	System.out.println("Constructed Tree is (Inorder Traversal):");
	printTree(root);
}
}

Output

Constructed Tree is (Inorder Traversal): 
D B E A F C

Python Programming

# Class for a node
# having an integer value, data
# and two pointers
# to store the references of the
# left and right children
class Node:
	
	def __init__(self, x):
		
		self.data = x
		self.left = None
		self.right = None

# function to build a binary tree
# from the given 2 arrays of integers, 
# inorder & preorder.
def convertBinaryTree(inn, pre, inStrt, inEnd):
	
	global preIndex, mp

	if (inStrt > inEnd):
		return None

	# create a new node and 
	# assign it the value of the current node
	# using the preIndex.
	# Update the preIndex variable
	# so that it can be used for next recursive calls.
	curr = pre[preIndex]
	preIndex += 1
	tNode = Node(curr)

	# return if the new created node does not have children.
	if (inStrt == inEnd):
		return tNode

	# otherwise, compute its height
	# in the inorder traversal.
	inIndex = mp[curr]

	# build left and right subtrees, with the help of 
	# inIndex in the inorder array.
	tNode.left = convertBinaryTree(inn, pre, inStrt,
						inIndex - 1)
	tNode.right = convertBinaryTree(inn, pre, inIndex + 1,
							inEnd)

	return tNode

# wrapper function for the convertBinaryTree function 
# that creates a map 
def convertBinaryTreeWrap(inn, pre, lenn):
	
	global mp
	
	# hold the indices of all elements in
	# the unorderd map.
	for i in range(lenn):
		mp[inn[i]] = i

	return convertBinaryTree(inn, pre, 0, lenn - 1)

# function to print the 
# constructed tree.
def printTree(node):

	if (node == None):
		return
		
	printTree(node.left)
	print(node.data, end = " ")
	printTree(node.right)

# Driver code
if __name__ == '__main__':
	
	mp = {}
	preIndex = 0

	inn = [ 'D', 'B', 'E', 'A', 'F', 'C' ]
	pre = [ 'A', 'B', 'D', 'E', 'C', 'F' ]
	lenn = len(inn)

	root = convertBinaryTreeWrap(inn, pre,lenn)


	print("Constructed Tree is (Inorder Traversal):")
	
	printTree(root)

Output

Constructed Tree is (Inorder Traversal): 
D B E A F C

C# Programming

using System;
using System.Collections.Generic;

// Class for a node
// having an integer value, data
// and two pointers
// to store the references of the
// left and right children
public class Node
{
	public char data;
	public Node left, right;

	public Node(char d)
	{
		data = d;
		left = right = null;
	}
}
public class Tree
{
	public static Node root;

	// hold the indices of all elements in
	// the unorderd map.
	static Dictionary<char,int> mp = new Dictionary<char,int>();
	static int preIndex = 0;

	// function to build a binary tree
	// from the given 2 arrays of integers, 
	// inorder & preorder.
	static Node convertBinaryTree(char[] In, char[] pre,
						int inStrt, int inEnd)
	{
		if(inStrt > inEnd)
		{
			return null;
		}
	
		// create a new node and 
		// assign it the value of the current node
		// using the preIndex.
		// Update the preIndex variable
		// so that it can be used for next recursive calls.
		char curr = pre[preIndex++];
		Node tNode;
		tNode = new Node(curr);
	
		// return if the new created node does not have children.
		if(inStrt == inEnd)
		{
			return tNode;
		}
	
		// otherwise, compute its height
		// in the inorder traversal.
		int inIndex = mp[curr];
	
		// build left and right subtrees, with the help of 
		// inIndex in the inorder array.
		tNode.left = convertBinaryTree(In, pre, inStrt, inIndex - 1);
		tNode.right = convertBinaryTree(In, pre, inIndex + 1, inEnd);
		return tNode;
	}

	// wrapper function for the convertBinaryTree function 
	// that creates a map 
	public static Node convertBinaryTreeWrap(char[] In, char[] pre, int len)
	{
		for(int i = 0; i < len; i++)
		{
			mp.Add(In[i], i);
		}
		return convertBinaryTree(In, pre, 0, len - 1);
	}

	// function to print the 
	// constructed tree.
	static void printInorder(Node node)
	{
		if(node == null)
		{
			return;
		}
		printInorder(node.left);
		Console.Write(node.data + " ");
		printInorder(node.right);
	}

	static public void Main (){
		char[] In = {'D', 'B', 'E', 'A', 'F', 'C'};
		char[] pre = {'A', 'B', 'D', 'E', 'C', 'F'};
		int len = In.Length;
		Tree.root = convertBinaryTreeWrap(In, pre, len);
	
		Console.WriteLine("Constructed Tree is (Inorder Traversal):");
		printInorder(Tree.root);
	}
}

Output

Constructed Tree is (Inorder Traversal): 
D B E A F C

Complexity Analysis:

Time Complexity : O(n) where n is the number of nodes of the Binary Tree.

Wrapping Up!

In this article, we have learned an amazing concept of Binary Trees. Binary Trees are one of the most important data structures and are usually asked in the top interview questions as well. “Construct a Binary Tree from Inorder and Preorder traversals” is a popular as well as a very important problem that has been asked in various interview questions. In this article, we have included proper examples with detailed explanations for a better understanding for you. We also learned about how we should think of a solution and then make optimizations in our code for such kinds of problems.

We also discussed two well-explained approaches along with some suitable examples to solve this problem. We also covered in detail how both of the approaches work and what is the significance of all of them. We discussed their time complexity along with a proper explanation. Different programmers prefer different languages for coding. So, we made sure that all our readers could refer to this article. That’s why this article also contains well-explained codes for all the approaches in the three most popular languages, which are c++, Java, C# and Python , along with their respective outputs attached to the article for a better understanding of a wide range of our readers.

We sincerely hope that this article has walked you through some deep and important concepts of Binary Trees and how we should approach such kinds of problems. We surely wish you to keep up your practice and crack all the questions easily. With this, we are wrapping up this article.

Happy Learning!

People are also reading:

• Stack vs Heap
• Types of Data Structure
• Tree vs Graph
• Global vs Local Variables
• What is Data Structure?
• Algorithms Basics
• Asymptotic Analysis
• DSA – Greedy Algorithms
• DSA – Divide and Conquer
• DSA – Dynamic Programming